1.已知集合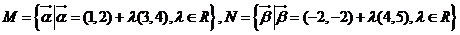 ,则
,则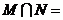 ( )
( )
A.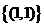 B.
B.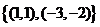 C.
C.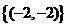 D.
D. 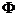
2.设复数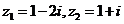 ,则复数
,则复数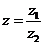 在复平面内对应的点位于( )
在复平面内对应的点位于( )
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3.已知等差数列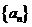 的前n项和为
的前n项和为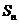 ,且满足
,且满足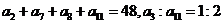 ,则
,则 等于( )
等于( )
A.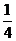 B.
B.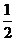 C.1
D.2
C.1
D.2
4.某高三年级的三个班级去甲、乙、丙、丁四个工厂进行社会实践,其中工厂甲必须有班级去,每班去何工厂可自由选择,则不同的分配方案是 ( )
A. 16种 B. 18种 C. 37种 D. 48种
5.若函数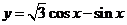 的图象向右平移
的图象向右平移 (
(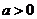 )个单位后,所得到的图象关于y轴对称,则
)个单位后,所得到的图象关于y轴对称,则 的最小值为(
)
的最小值为(
)
A.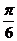 B.
B.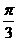 C.
C.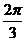 D.
D.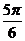
6.函数 的图象与函数
的图象与函数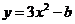 的图象有三个不相同的交点,则实数
的图象有三个不相同的交点,则实数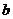 的取值范围是( )
的取值范围是( )
A.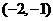 B.
B.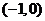 C.
C.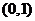 D.
D.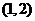
7.如果把直线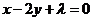 向左平移1 个单位,再向下平移2个单位,便与圆
向左平移1 个单位,再向下平移2个单位,便与圆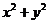
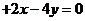 相切,则实数
相切,则实数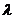 的值是( )
的值是( )
A.13或3
B.13或
8.已知点P是椭圆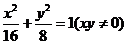 上的动点,
上的动点,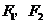 为椭圆的两个焦点,
为椭圆的两个焦点,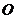 是坐标原点,若
是坐标原点,若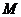 是
是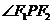 的角平分线上一点,且
的角平分线上一点,且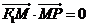 ,则
,则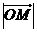 的取值范围是( )
的取值范围是( )
A.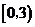 B.
B.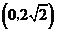 C.
C.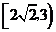 D.
D.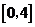
9. 正四面体A―BCD中,E在棱AB上,F在棱CD上,使得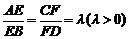 ,设
,设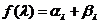 ,
,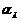 与
与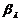 分别表示EF与AC,BD所成的角,则( )
分别表示EF与AC,BD所成的角,则( )
A.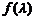 是(0,+∞)上的增函数
B.
是(0,+∞)上的增函数
B.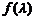 是(0,+∞)上的减函数
是(0,+∞)上的减函数
C.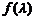 在(0,1)上递增,在(1,+∞)上递减
D.
在(0,1)上递增,在(1,+∞)上递减
D.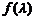 是(0,+∞)上的常数函数
是(0,+∞)上的常数函数
10. 定义在 上的函数
上的函数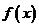 满足
满足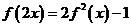 ,现给定下列几个命题:
,现给定下列几个命题:
①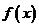 不可能是奇函数;②
不可能是奇函数;②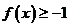 ;③
;③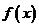 不可能是常数函数;④若
不可能是常数函数;④若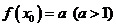 ,则不存在常数
,则不存在常数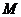 ,使得
,使得 成立.在上述命题中错误命题的个数为 ( )
成立.在上述命题中错误命题的个数为 ( )
A. 1
B.
第 Ⅱ 卷(非选择题 共100分)
11.已知方程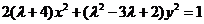 表示椭圆,则
表示椭圆,则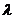 的取值范围为 .
的取值范围为 .
12.将函数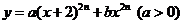 向右平移一个单位后是一个偶函数,则
向右平移一个单位后是一个偶函数,则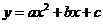 的单调递减区间为
.
的单调递减区间为
.
13.已知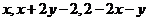 是数列
是数列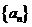 中的三个非负项,则
中的三个非负项,则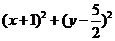 的最小值为
.
的最小值为
.
14.函数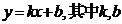 (
(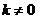 )是常数,其图象是一条直线,称这个函数为线性函数.而对于非线性可导函数
)是常数,其图象是一条直线,称这个函数为线性函数.而对于非线性可导函数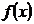 ,在已知点
,在已知点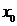 附近一点
附近一点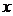 的函数值
的函数值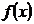 ,可以用如下方法求其近似代替值:
,可以用如下方法求其近似代替值: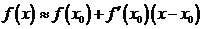 .利用这一方法,对于实数
.利用这一方法,对于实数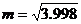 ,取
,取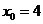 ,则
,则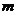 的近似代替值
的近似代替值
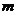 .(填“>”或“<”或“=”)
.(填“>”或“<”或“=”)
 15.如右图所示的
15.如右图所示的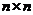 的数表,满足每一行都是公差
的数表,满足每一行都是公差
为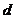 的等差数列,每一列都是公比为
的等差数列,每一列都是公比为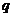 的等比数列.
的等比数列.
已知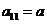 ,则
,则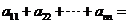 .
.
16.(本题满分12分)
已知向量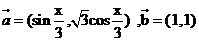 ,函数
,函数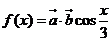 .
.
(1)将f(x)写成 的形式,并求其图象的对称中心;
的形式,并求其图象的对称中心;
(2)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的取值范围及此时函数f(x)的值域.
17.(本题满分12分)现从放有标号分别为数字1、2、3、4、5的5 张卡片的盒子中,有放回地先后取两张卡片,设两卡片的标号分别为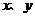 ,且设
,且设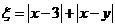 .
.
(1)求随机变量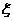 的最大值,并求取得此最大值的概率;
的最大值,并求取得此最大值的概率;
(2)求随机变量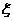 的分布列及其方差.
的分布列及其方差.
18.(本题满分12分)如图,四面体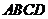 的各个面都是直角三角形,已知
的各个面都是直角三角形,已知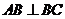 ,
,

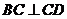 ,
,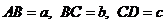 .
.
(1)若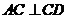 ,求证:
,求证: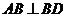 ;
;
(2)求四面体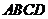 的表面积.
的表面积.
19.(本题满分13分)自然状态下的鱼类是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响. 用xn表示某鱼群在第n年年初的总量,n∈N*,且x1>0. 不考虑其它因素,设在第n年内鱼群的繁殖量及捕捞量都与xn成正比,死亡量与xn2成正比,这些比例系数依次为正常数a,b,c.
(Ⅰ)求xn+1与xn的关系式;
(Ⅱ)猜测:当且仅当x1,a,b,c满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
(Ⅲ)设a=2,c=1,为保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度b的最大允许值是多少?证明你的结论.
20.(本题满分13分)双曲线C与椭圆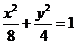 有相同的焦点,直线y=
有相同的焦点,直线y=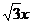 为C的一条渐近线.
为C的一条渐近线.
(1)求双曲线C的方程;
(2)过点P(0,4)的直线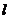 ,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当
,交双曲线C于A,B两点,交x轴于Q点(Q点与C的顶点不重合).当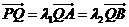 ,且
,且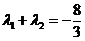 时,求Q点的坐标.
时,求Q点的坐标.
21.(本题满分13分)已知函数 ,
,
(1)试确定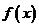 的单调性;
的单调性;
(2)数列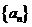 满足
满足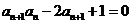 ,且
,且 ,
,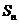 表示
表示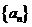 的前
的前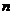 项之和
项之和
①求数列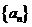 的通项; ②求证:
的通项; ②求证: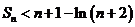 .
.
‘
2009年普通高等学校招生全国统一考试(荆中模拟卷)

