12.将函数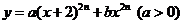 向右平移一个单位后是一个偶函数,则
向右平移一个单位后是一个偶函数,则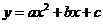 的单调递减区间为
.
的单调递减区间为
.
- 答案
1~10:C C B C A B A B D A
11、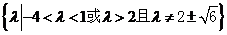 12、
12、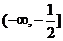 13、
13、 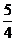 14、>
14、>
15、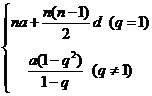 (提示:15.
(提示:15.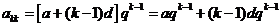 ,又
,又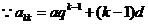
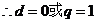 )
)
16.解:(1)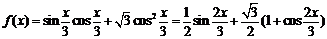
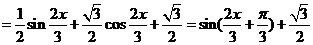 ………3(分)
………3(分)
由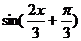 =0即
=0即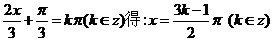
即对称中心为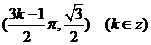 …………6(分)
…………6(分)
(2)已知b2=ac
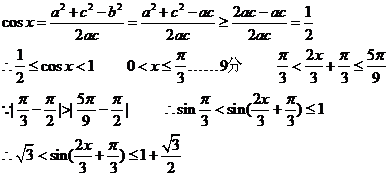
即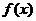 的值域为
的值域为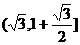 综上所述,
综上所述,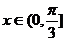 ,故
,故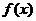 值域为
值域为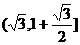 …12(分)
…12(分)
17.解:(1)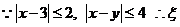 的最大值为6,此时有
的最大值为6,此时有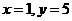 或
或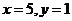 ,故所求的概率为
,故所求的概率为
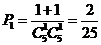 .
…………5(分)
.
…………5(分)
(2)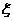 的所有可能取值是0,1,2,3,4,5,6.其分布列为:
的所有可能取值是0,1,2,3,4,5,6.其分布列为:
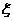
0
1
2
3
4
5
6
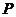
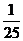
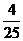
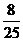
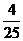
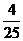
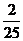
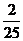
……………10(分)
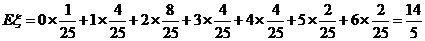 ……12(分)
……12(分)
18.解:(1)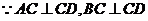
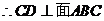 ,
又
,
又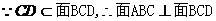
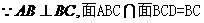
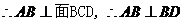 …………5(分)
…………5(分)
(2)当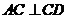 时,则
时,则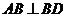
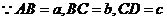
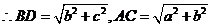
其表面积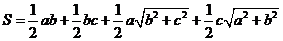
当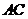 与
与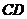 不垂直时,则
不垂直时,则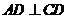 ,否则由(1)知
,否则由(1)知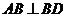 ,可得
,可得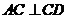 (矛盾).
(矛盾).
当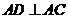 时,
时,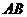 与
与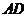 不能垂直,否则
不能垂直,否则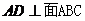
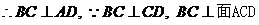 ,从而
,从而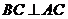 ,与
,与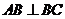 矛盾.
矛盾.
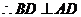 ,从而可得
,从而可得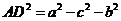 …………①
…………①
由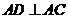 得,
得,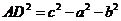 …………②
…………②
根据①、②得: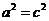 ,从而导致
,从而导致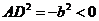 矛盾.
矛盾.
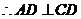 ,从而得到
,从而得到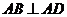
当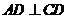 时,
时,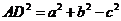
当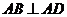 时,
时,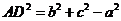
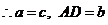 ,即四面体的各个面是全等的三角形.
,即四面体的各个面是全等的三角形.
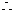 其表面积为
其表面积为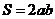 .
……………12(分)
.
……………12(分)
19.解:(I)从第n年初到第n+1年初,鱼群的繁殖量为axn,被捕捞量为bxn,死亡量为
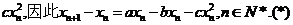
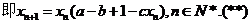 …………(3分)
…………(3分)
(II)若每年年初鱼群总量保持不变,则xn恒等于x1, n∈N*,从而由(*)式得
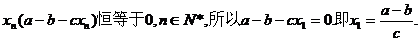 因为x1>0,所以a>b.
因为x1>0,所以a>b.
猜测:当且仅当a>b,且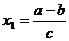 时,每年年初鱼群的总量保持不变.
……(6分)
时,每年年初鱼群的总量保持不变.
……(6分)
(Ⅲ)若b的值使得xn>0,n∈N*, 由xn+1=xn(3-b-xn), n∈N*, 知0<xn<3-b, n∈N*, 特别地,有0<x1<3-b. 即0<b<3-x1,而x1∈(0, 2),所以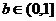
由此猜测b的最大允许值是1. ……………(10分)
下证 当x1∈(0, 2) ,b=1时,都有xn∈(0, 2), n∈N*
①当n=1时,结论显然成立.
②假设当n=k时结论成立,即xk∈(0, 2),则当n=k+1时,xk+1=xk(2-xk)>0.
又因为xk+1=xk(2-xk)=-(xk-1)2+1≤1<2,所以xk+1∈(0, 2),故当n=k+1时结论也成立.
由①、②可知,对于任意的n∈N*,都有xn∈(0,2).
综上所述,为保证对任意x1∈(0, 2), 都有xn>0, n∈N*,则捕捞强度b最大允许值是1.…(13分)
20. 解:(1)设双曲线方程为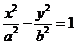 ,由椭圆
,由椭圆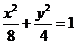 求得两焦点为
求得两焦点为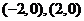 ,
,
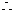 对于双曲线
对于双曲线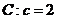 ,又
,又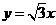 为双曲线
为双曲线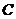 的一条渐近线
的一条渐近线
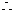
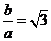 解得
解得 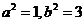 ,
,
 双曲线
双曲线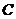 的方程为
的方程为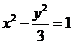 ……………(5分)
……………(5分)
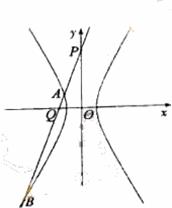
(2)解法一:
由题意知直线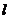 的斜率
的斜率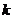 存在且不等于零。
存在且不等于零。
设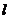 的方程:
的方程: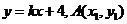 ,
,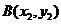 则
则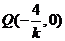
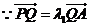
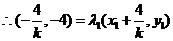
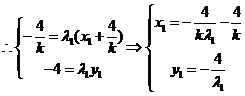
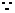
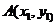 在双曲线
在双曲线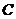 上,
上,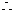
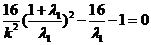
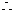
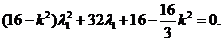
同理有: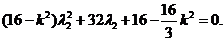
若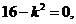 则直线
则直线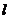 过顶点,不合题意.
过顶点,不合题意.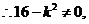
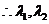 是二次方程
是二次方程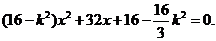 的两根.
的两根.
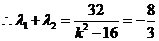
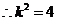 ,
,
此时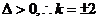 .
.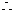 所求
所求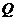 的坐标为
的坐标为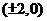 .
…………(13分)
.
…………(13分)
解法二:由题意知直线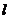 的斜率
的斜率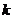 存在且不等于零
存在且不等于零
设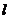 的方程:
的方程: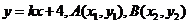 ,则
,则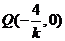 .
.
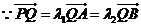 ,
,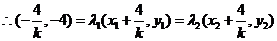 .
.
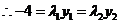 ,
,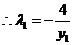 ,
,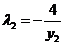 ,
,
又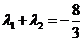 ,
,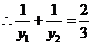 ,即
,即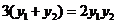
将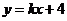 代入
代入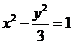 得
得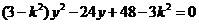
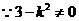 ,否则
,否则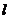 与渐近线平行。
与渐近线平行。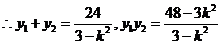 。
。
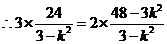
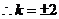
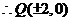 .
.
21.(1)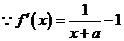
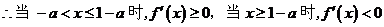
故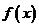 在
在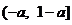 上是单调递增函数,在
上是单调递增函数,在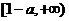 上是单调递减函数
……4(分)
上是单调递减函数
……4(分)
(2)①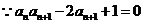
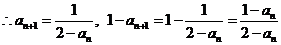
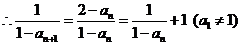
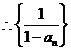 是公差为1的等差数列,且首项为
是公差为1的等差数列,且首项为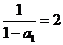
故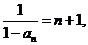
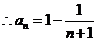 ……………9(分)
……………9(分)
②由(1)知,当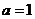 时,
时,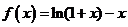 在
在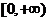 是单调递减函数,又
是单调递减函数,又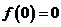 ,
,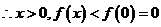 ,即
,即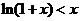
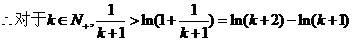 .
.

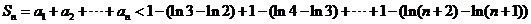
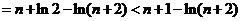 ………13(分)
………13(分)

