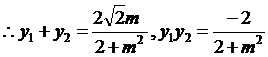13.若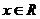 ,则
,则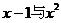 的大小关系是_______.
的大小关系是_______.
14.椭圆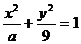 的离心率为
的离心率为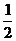 ,则
,则 =________ .
=________ .
15.圆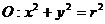
 内一点
内一点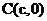 ,A、B在⊙O上,且
,A、B在⊙O上,且 ,AB的中点P的轨迹方程为_______________.
,AB的中点P的轨迹方程为_______________.
16.已知下列四命题
①在直角作标系中,如果点P在曲线上,则P点坐标一定是这曲线方程的解;
②平面内与两个定点F1 ,F2的距离的差的绝对值等于常数的点的轨迹叫做双曲线;
③角α一定是直线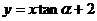 的倾斜角;
的倾斜角;
④直线 关于
关于 轴对称的直线方程为
轴对称的直线方程为
其中正确命题的序号是 .(注:把你认为正确命题的序号都填上)
17.(本小题10分)
已知椭圆C的焦点F1(-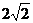 ,0)和F2(
,0)和F2(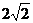 ,0),长轴长6,设直线
,0),长轴长6,设直线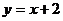 交椭圆C于A、B两点,求线段AB的中点坐标。
交椭圆C于A、B两点,求线段AB的中点坐标。
18. (本题12分)
直线 经过两条直线
经过两条直线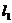 :
: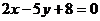 和
和
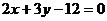 的交点,且分这两条直线与
的交点,且分这两条直线与 轴围成的面积为
轴围成的面积为 两部分,求直线
两部分,求直线 的一般式方程。
的一般式方程。
19.(本题10分)
已知A(-2,0),B(2,0),动点P与A、B两点连线的斜率分别为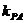 和
和 ,且满足
,且满足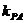 ・
・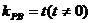
(1)求动点P的轨迹C的方程;
(2)当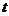 变化时,轨迹C如何变化。
变化时,轨迹C如何变化。
20.(本题12分)
已知两圆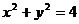 和
和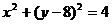
(1) 若两圆圆心在直线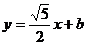 的两侧,求实数
的两侧,求实数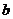 的取值范围;
的取值范围;
(2)求经过点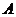 (0,5)且和两圆都没有公共点的直线的斜率
(0,5)且和两圆都没有公共点的直线的斜率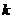 的范围。
的范围。
21.(本题12分)
已知椭圆的中心是坐标原点O,焦点在 轴上.
轴上.
(1)若椭圆的离心率为 ,且椭圆上的点到其准线的最短距离为
,且椭圆上的点到其准线的最短距离为 ,求此椭圆的方程;
,求此椭圆的方程;
(2)若过左焦点 的直线
的直线 交椭圆于A、B两点,且
交椭圆于A、B两点,且 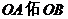 .在(1)的条件下,求直线
.在(1)的条件下,求直线 的方程。
的方程。
22.(本题12分)
已知点A(0, 1),点B(2,3)及曲线C:y=x2+mx+2 (m∈R),
(1) 求证曲线C 过定点,并求此定点坐标;
(2) 若曲线C和线段AB有两个交点,求m的取值范围;
(3) 当m为何值时,可使曲线C在线段AB上所截得的弦最长?并求出这个最大弦长。
2007―2008年度第一学期高二年级第1次月考
数 学 试 卷(理科)答案
1.D 2.C 3.B 4.B 5.D
6.B 7.D 8.C 9.B 10.C
11.C 12.A
13,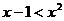 14,
14,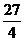 或12
或12
15,
16,① ④
17,解:由题意知: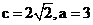 ,故
,故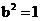 ,焦点在
,焦点在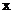 轴上,
轴上,
∴椭圆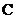 的方程为
的方程为
设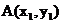 ,
, ,
,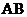 的中点为
的中点为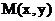 ,∵
,∵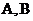 两点在椭圆上,
两点在椭圆上,
∴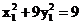 ,
, ,
,
两式相减即得: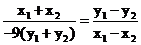 即:
即: ①
①
又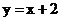 ②
由①②可得:
②
由①②可得: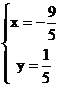 ∴
∴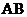 的中点坐标为
的中点坐标为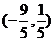
18、:解:由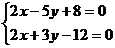
得两直线交点的坐标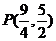 ,
,
又由题意知S1:S2=2:3或3:2
所以 由A (-4,0),B(6,0) 根据定比分点公式得
由A (-4,0),B(6,0) 根据定比分点公式得
M(0,0)或M(2,0),所以所求直线的方程就是经过P和M两点的直线方程
所以所求直线的一般式方程是
19,解:(1)设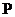 点的坐标为
点的坐标为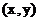 ,由题意知
,由题意知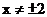
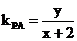 ,
, 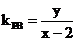
∵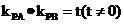 ∴
∴
所以动点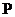 的轨迹方程为
的轨迹方程为 
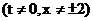
(2)动点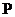 的轨迹方程为
的轨迹方程为
1)若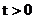 ,则轨迹
,则轨迹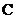 是焦点在
是焦点在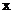 轴上的双曲线(不含
轴上的双曲线(不含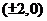 )
)
2)若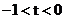 ,则轨迹
,则轨迹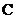 是焦点在
是焦点在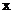 轴上的椭圆(不含
轴上的椭圆(不含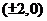 )
)
3)若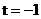 ,则轨迹
,则轨迹 是以
是以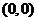 为圆心,以2为半径的圆(不含
为圆心,以2为半径的圆(不含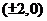 )
)
4)若 ,则轨迹
,则轨迹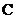 是焦点在
是焦点在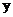 轴上的椭圆(不含
轴上的椭圆(不含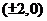 )
)
20、解:(1)将已知直线写成一般式为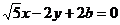
两圆的圆心为(0,0)和(0,8)
由题意知,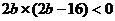
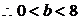
(2)设所求的直线方程为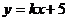 ,即
,即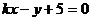
依题意得
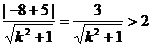
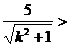
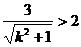 ,故只要解
,故只要解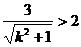 即可
即可
解得: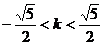
21.解:(1)设椭圆的方程为 ,则有
,则有

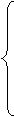
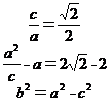 ,解得
,解得 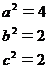 ,
,
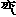 所求椭圆方程为
所求椭圆方程为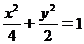
(2)(I)由(1)知左焦点 为(
为(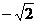 ,0)
,0)
设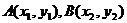 ,则由
,则由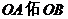 ,得
,得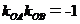
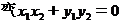 , …………………………………4分
, …………………………………4分
由题意知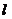 的斜率不等于零,故可设
的斜率不等于零,故可设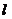 :
: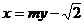
 由
由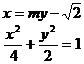 ,得
,得 --①…………6分
--①…………6分
又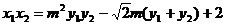
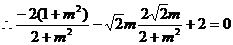 ……………………………7分
……………………………7分
即 ,所以
,所以
代入①中的 ,易知
,易知 ,
, 
 适合
适合
 综上所求直线
综上所求直线 方程为
方程为
 即
即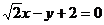 或
或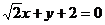
22,解:(1)曲线C的方程即为: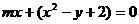
由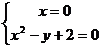 得:
得: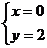 故曲线C过定点
故曲线C过定点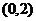
(2)线段AB的方程为: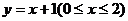
由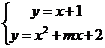 消去
消去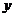 ,整理得
,整理得
由题意知方程  在
在 上有两个不等的实根。
上有两个不等的实根。
令 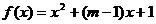 △
△
则  得
得 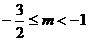
(3)由(2)知: 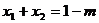 ,
, 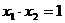
所以 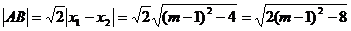
对于 , 在
, 在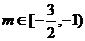 内单调递减,
内单调递减,
所以当 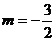 时,
时,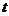 有
有