(1)函数 的定义域是
的定义域是
A. B.(1,2)
C.(2,+∞) D.(-∞,2)
B.(1,2)
C.(2,+∞) D.(-∞,2)
(2)已知 ,则
,则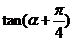 的值是
的值是
A. B.
B. D.
D.
(3)设复数 ,则z等于
,则z等于
A.2 B.-
(4)下列各题中,使M是N成立的充要条件的一组是
A.M:a>b,N:ac2>bc2 B.M:a>b,c>d,N:a-d>b-c
C.M:a>b>0,c>d>0,N:ac>bd D.M:|a-b|=|a|+|b|,N:ab≤0
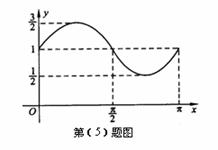
(5)函数 的图象如图所示,则它的解析式是
的图象如图所示,则它的解析式是
 A.
A. B.
B.
C.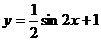 D.
D.
(6) 展开式的第四项等于7,
展开式的第四项等于7,
则
A.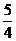 B.
B. C.
C. D.
D.
(7)设点A在圆 上,点B在直线
上,点B在直线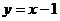 上,则|AB|的最小值是
上,则|AB|的最小值是
A. B.
B.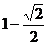 C.
C. D.
D.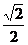
(8)设 ,
, ,给出M到N的映射
,给出M到N的映射 ,则点
,则点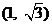 的象
的象 的最小正周期为
的最小正周期为
A.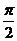 B.
B. C.
C. D.
D.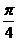
(9)设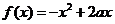 与
与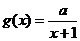 在区间
在区间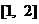 上都是减函数,则a的取值范围是
上都是减函数,则a的取值范围是
A. B.
B.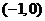 C.
C.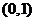 D.
D.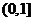
(10)由0,1,2,3,4,5六个数字组成数字不重复且百位数字不是5的5位数的个数为
A.504个 B.408个 C.720个 D.480个
(11)矩形ABCD的对角线AC、BD成 角,把矩形所在的平面以AC为折痕,折成一个直二面角D-AC-B,连结BD,则BD与平面ABC所成角的正切值为
角,把矩形所在的平面以AC为折痕,折成一个直二面角D-AC-B,连结BD,则BD与平面ABC所成角的正切值为
A. B.
B. C.
C.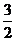 D.
D.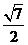
(12)已知点M(-3,0),N(3,0),B(1,0),圆C与直线MN切于点B,过M、N与圆C相切的两直线相交于点P,则P点的轨迹方程为
A.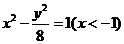 B.
B.
C. D.
D.
平顶山市2008届高三调研考试
理科数学
第Ⅱ卷
注意事项:
1.答题前,考生先用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚.
2.本卷共10小题,共90分.
一
二
三
总 分
17
18
19
20
21
22
(13)已知 ,
,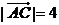 ,
, 与
与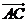 的夹角为60°,则
的夹角为60°,则 与
与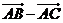 的夹角余弦为 .
的夹角余弦为 .
(14)设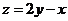 ,式中变量
,式中变量 ,
,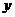 满足
满足 ,则
,则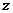 的最小值为_________.
的最小值为_________.
(15)设正四棱锥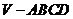 的所有棱长都是
的所有棱长都是 ,并且A、B、C、D、V都在一个球面上,则这个球面的面积为_______________.
,并且A、B、C、D、V都在一个球面上,则这个球面的面积为_______________.
(16)设 上的函数
上的函数 满足
满足 ,当
,当 时,
时, ,那么
,那么 .
.
(17)(本小题满分10分)
 已知
已知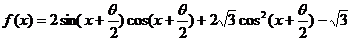 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)设 ,且函数
,且函数 为偶函数,求满足
为偶函数,求满足 ,
, 的x的集合.
的x的集合.
(18)(本小题满分12分)
 有一种舞台灯,外形是正六棱柱,在其每一个侧面上安装5只颜色各异的彩灯,假若每只灯正常发光的概率为
有一种舞台灯,外形是正六棱柱,在其每一个侧面上安装5只颜色各异的彩灯,假若每只灯正常发光的概率为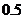 . 若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面.假定更换一个面需要100元,用ξ表示维修一次的费用.
. 若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面.假定更换一个面需要100元,用ξ表示维修一次的费用.
(Ⅰ)求恰好有2个面需要维修的概率;
(Ⅱ)写出ξ的分布列,并求ξ的数学期望.
(19)(本大题满分12分)
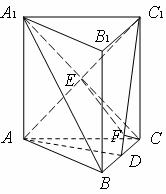
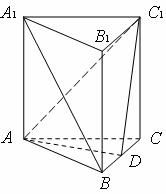 如图,在正三棱柱ABC-A1B
如图,在正三棱柱ABC-A1B
 (Ⅰ)求证:A1B∥平面AC1D;
(Ⅰ)求证:A1B∥平面AC1D;
(Ⅱ)求二面角C-AC1-D的大小.
(20)(本小题满分12分)
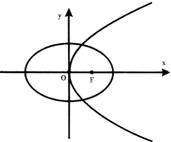
 设椭圆
设椭圆 的中心在原点,其右焦点与抛物线
的中心在原点,其右焦点与抛物线 :
: 的焦点F重合,过点F与x轴垂直的直线与
的焦点F重合,过点F与x轴垂直的直线与 交于A、B两点,与
交于A、B两点,与 交于C、D两点,已知
交于C、D两点,已知 .
.
 (Ⅰ)求椭圆
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点F的直线l与 交于M、N两点,与
交于M、N两点,与 交于P、Q两点,若
交于P、Q两点,若 ,求直线l的方程.
,求直线l的方程.
(21)(本小题满分12分)
设数列 的各项都是正数,且对任意
的各项都是正数,且对任意 都有
都有 成立,其中
成立,其中 是数列
是数列 的前n项和.
的前n项和.
 (Ⅰ)求数列
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设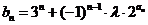 (
( ),试确定
),试确定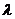 的值,使得对任意
的值,使得对任意 ,都有
,都有 成立.
成立.
(22)(本小题满分12分)
设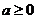 ,函数
,函数 ,
, .
.
 (I)当
(I)当 时,求
时,求 的最小值;
的最小值;
(II)假设存在 ,使得|
,使得| |<1成立,求
|<1成立,求 的取值范围.
的取值范围.
平顶山市2008届高三调研考试
理科数学答案
(17)解:(Ⅰ)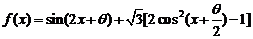
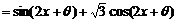 =
=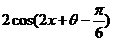
或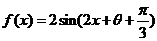 ,
…………3分
,
…………3分
所以, 的最小正周期
的最小正周期 ;
…………5分
;
…………5分
(Ⅱ)当 时,f(x)为偶函数 .
…………7分
时,f(x)为偶函数 .
…………7分
由 ,得
,得 ,所以
,所以 ,
…………8分
,
…………8分
 ,
…………9分
,
…………9分
所以,所求x的集合为 . ……………10分
. ……………10分
(18)解:(Ⅰ)因为一个面不需要维修的概率为 ,
,
所以一个面需要维修的概率为 .
……3分
.
……3分
因此,六个面中恰好有2个面需要维修的概率为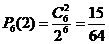 . ……6分
. ……6分
(Ⅱ)因为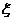 ~
~ ,又
,又 ,
, ,
,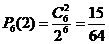 ,
,
 ,
, ,
, ,
,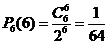 ,
,
所以维修一次的费用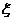 的分布为:
的分布为:
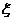
0
100
200
300
400
500
600
P

……10分
因为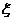 ~
~ ,所以
,所以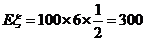 元.
……12分
元.
……12分
(19)解:(Ⅰ)∵ABC-A1B
∴ AD⊥BC, ∴ D是BC的中点. ……3分
连结AC1与A
∴A1B∥DE,又DE在平面AC1D内,∴A1B∥平面AC1D. ……6分
 (Ⅱ)作CF⊥C1D于F,则CF⊥平面AC1D,连结EF,∵CE⊥AC1
(Ⅱ)作CF⊥C1D于F,则CF⊥平面AC1D,连结EF,∵CE⊥AC1
∴ EF⊥AC1,∴ 则∠CEF就是二面角C-AC1-D的平面角. ……8分∵ ,
, , ……10分
, ……10分
∴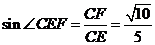 ,
,
即,二面角C-AC1-D的
大小为 .
……12分
.
……12分
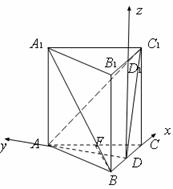 方法二:设D1是B
方法二:设D1是B
DA为y轴,DD1为z轴建立空间直角坐标系
(如图), ……7分
并设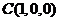 ,则
,则 ,
, ,
, ,∵AC的中点为
,∵AC的中点为 ,
,
∴ ,
……8分
,
……8分
∴平面AC .
……9分
.
……9分
设平面AC1D的法向量为 ,∵
,∵ ,
,
∴ ,∴
,∴ , ……10分
, ……10分
∴ ,
……11分
,
……11分
因此,二面角C-AC1-D的大小为 .
……12分
.
……12分
(20)解:(Ⅰ)由抛物线方程,得焦点F(1,0).
设椭圆 的方程:
的方程: .
…………1分
.
…………1分
解方程组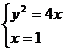 得C(1,2),D(1,-2). …………2分
得C(1,2),D(1,-2). …………2分
由于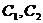 都关于x轴对称,
都关于x轴对称,
∴ ,
, , ∴
, ∴ . …………3分
. …………3分
∴ 又
又 ,
,
因此, ,解得
,解得 并推得
并推得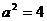 .
…………5分
.
…………5分
故椭圆 的方程为
的方程为 .
…………6分
.
…………6分
(Ⅱ)设l:x=ty+1,解方程组 ,
,
消元得: ,
, ,
,
∴ .
…………8分
.
…………8分
再解方程组 ,
,
得: ,
, ,
,
∴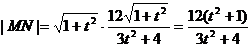 .
…………10分
.
…………10分
由 ,即
,即 , ∴
, ∴ . …………11分
. …………11分
故直线l的方程为: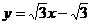 或
或 .
…………12分
.
…………12分
(21)解:(Ⅰ)∵  ,∴
,∴  ,
,
∴ ,
,
∴  .
…………3分
.
…………3分
∴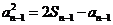 , ∴
, ∴ ,
,
∴ , ∴
, ∴ 是以1为首项,1为公差的等差数列.
是以1为首项,1为公差的等差数列.
∴ .
…………6分
.
…………6分
注:用数学归纳法给出 应同步给分.
应同步给分.
(Ⅱ)∵ ,
,
∴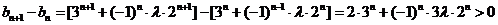 ,
,
∴ ,∴
,∴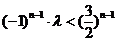 对一切
对一切 成立.…………9分
成立.…………9分
当n为奇数时,
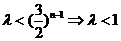 ,
,
当n为偶数时,
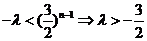 ,
,
∴ .
…………12分
.
…………12分
(22)解:(Ⅰ)∵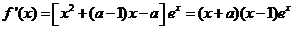 , ……2分
, ……2分
∵ ,所以
,所以 的极值点为
的极值点为 ,
, ,
,
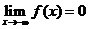 ,
, ,
, 的略图如下图.
的略图如下图. 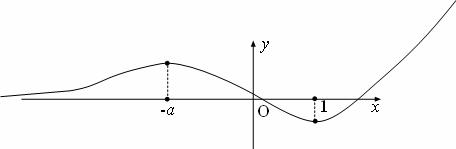
所以, 的最小值是
的最小值是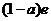 .
……6分
.
……6分
(II)由(Ⅰ)知 在
在 的值域是,
的值域是,
当 时,为
时,为 ,当
,当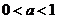 时,为
时,为 .
……8分
.
……8分
而 在
在 的值域是为
的值域是为 ,
……9分
,
……9分
所以,当 时,令
时,令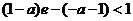 ,并解得
,并解得 ,
,
当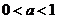 时,令
时,令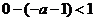 ,无解.
,无解.
因此, 的取值范围是
的取值范围是 .
……12分
.
……12分


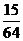

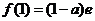 ,
,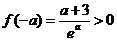 ,
,