1.已知集合P={0,b},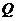 ={x|x2-3x<0,
={x|x2-3x<0,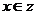 },若P
},若P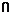
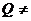
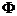 ,则b等于
,则b等于
A.1 B
2.若函数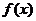 的反函数
的反函数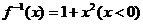 ,则
,则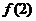 的值为
的值为
A.1 B.-1 C.1或-1 D.-5
3.若双曲线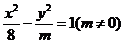 的一条准线与抛物线
的一条准线与抛物线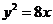 的准线重合,则双曲线的离心率为
的准线重合,则双曲线的离心率为
A.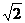 B.
B. C.4 D.
C.4 D.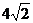
4、若曲线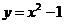 与
与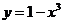 在
在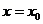 处的切线互相垂直,则
处的切线互相垂直,则 的值为
的值为
A. B.
B.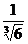 C.
C.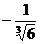 D.
D.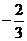 或0
或0
5.若 且
且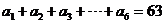 ,则实数m的值为
,则实数m的值为
A.1 B.-1 C.-3 D.1或-3
6.若点Q在直线b上,b在平面 内,则Q、b、
内,则Q、b、 之间的关系可写作
之间的关系可写作
A.Q b
b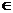
 B.
Q
B.
Q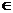 b
b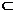
 C.Q
C.Q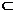 b
b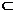
 D.Q
D.Q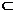 b
b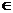

7.若函数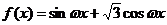 ,
,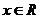 ,又
,又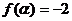 ,
, ,且
,且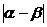 的最小值等于
的最小值等于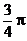 ,则正数
,则正数 的值为
的值为
A.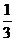 B.
B.
 C.
C.
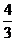 D.
D. 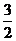
8.已知:O、A、B、C是不共线的四点,若存在一组正实数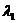 、
、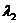 、
、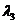 ,使
,使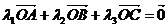 ,则三个角∠AOB、∠BOC、∠COA中
,则三个角∠AOB、∠BOC、∠COA中
A.有一个钝角 B.至少有两个钝角
C.至多有两个钝角 D.没有钝角
9.设A(x1,y1),B(4,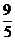 ),C(x2, y2)是右焦点为F的椭圆
),C(x2, y2)是右焦点为F的椭圆 上三个不同的点,则“
上三个不同的点,则“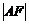 ,
,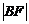 ,
,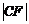 成等差数列”是“x1+x2=
成等差数列”是“x1+x2=
A.充要条件 B.必要而不充分条件
C.充分而不必要条件 D.既不充分也不必要条件
10.已知定义在R上的函数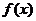 在
在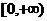 上是增函数,且
上是增函数,且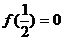 ,又函数
,又函数
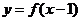 关于
关于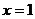 对称,则不等式
对称,则不等式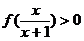 的解集是
的解集是
A. 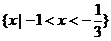 B.
B.

C. 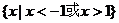 D.
D. 
11.圆心为(1,2)且与直线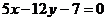 相切的圆的方程是
.
相切的圆的方程是
.
12.设实数x,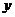 满足
满足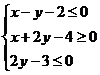 则
则 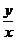 的最大值是
.
的最大值是
.
13.已知正方体的全面积是
14.已知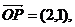
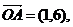
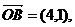 设M是直线OP上一点(O为坐标原点),那么使
设M是直线OP上一点(O为坐标原点),那么使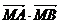 取最小值时的
取最小值时的 的坐标为 .
的坐标为 .
15.给出下列命题:
①对数函数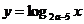 在
在 是增函数,则实数a的取值范围是
是增函数,则实数a的取值范围是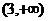 ;
;
②若不等式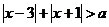 的解集为R,则实数a的取值范围是
的解集为R,则实数a的取值范围是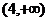 ;
;
③若方程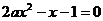 在(0,1)内恰有一解,则实数a的取值范围是
在(0,1)内恰有一解,则实数a的取值范围是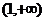 ;
;
④在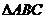 中,若AB=1,BC=2,则角C的取值范围是
中,若AB=1,BC=2,则角C的取值范围是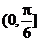 ,其中真命题的编号是
(写出所有真命题的编号).
,其中真命题的编号是
(写出所有真命题的编号).
 怀化市2008年高三第一次模拟考试统一检测试卷
怀化市2008年高三第一次模拟考试统一检测试卷
数学(文科)答题卷
登 分 栏
题号
一
二
三
总分
16
17
18
19
20
21
得分
一 、选择题(每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
11、 ; 12、 ;
13、 ; 14、 ; 15、 .
评卷人
得 分
16、(本题满分12分)
张华同学骑自行车上学途中要经过4个交叉路口,在各交叉路口遇到红灯的概率都是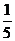 (假设各交叉路口遇到红灯的事件是相互独立的).
(假设各交叉路口遇到红灯的事件是相互独立的).
(1)求张华同学某次上学途中恰好遇到3次红灯的概率;
(2)求张华同学某次上学时,在途中首次遇到红灯前已经过2个交叉路口的概率.
评卷人
得 分
17.(本小题满分12分)
在等比数列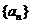 中,
中,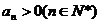 ,公比
,公比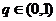 ,且
,且 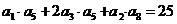 ,又
,又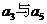 的等比中项为2.
的等比中项为2.
(1)求数列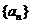 的通项公式;
的通项公式;
(2)设 ,数列
,数列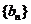 的前n项和为Sn,求
的前n项和为Sn,求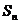 的最大值.
的最大值.
评卷人
得 分
评卷人
得 分
18. (本题满分12分)
已知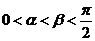 ,且
,且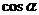 ,
,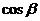 是方程
是方程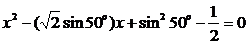 的两根.
的两根.
(1)求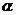 、
、 的值;
的值;
(2)求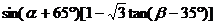 的值.
的值.
19.(本小题满分13分)
如图,在矩形ABCD中,AB=2,AD=1,E是CD的中点,以AE为折痕将△DAE向上折起,使D到D1,且平面D1AE⊥平面ABCE,连结D1B、D1C.
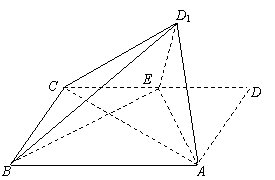 (1)求证:AD1⊥EB;
(1)求证:AD1⊥EB;
(2)求二面角D1-AB-E的大小;
(3)求点C到平面ABD1的距离.
评卷人
得 分
20.(本小题满分13分)'
已知函数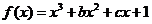 ,在区间
,在区间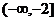 上单调递增,在区间
上单调递增,在区间 上单调递减,且
上单调递减,且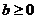 .
.
(1)求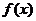 的表达式;
的表达式;
(2)设 ,若对任意的
,若对任意的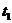 ,
,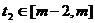 ,不等式
,不等式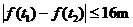 恒成立,求实数m的最小值.
恒成立,求实数m的最小值.
评卷人
得 分
21.(本小题满分13分)
如图, A为椭圆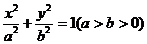 上的一个动点,弦AB、AC分别过焦点F1、F2,当AC垂直于x轴时,恰好有
上的一个动点,弦AB、AC分别过焦点F1、F2,当AC垂直于x轴时,恰好有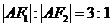 .
.
(1)求该椭圆的离心率;
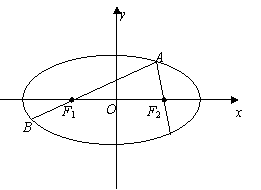 (2)设
(2)设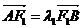 ,
,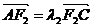 ,试判断
,试判断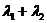 是否为定值?若是,则求出该定值;若不是,请说明理由
是否为定值?若是,则求出该定值;若不是,请说明理由 .
.
怀化市2008年高三第一次模拟考试检测试卷

