C. 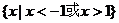 D.
D. 
- 答案
一、选择题(本大题共10小题,每小题5分,共50分;每个小题给出四个选项,只有一项符合要求)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
A
B
D
B
B
B
A
D
二、填空题(本大题共5个小题,每小题5分,共25分)。
11、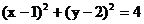 ;12、
;12、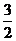 ;13、
;13、 ;14、(
;14、( );15、①③④
);15、①③④
三、解答题(本大题共6小题,共75分,解答题应写出必要的文字说明,证明过程或演算步骤).
16.解:(1)经过各交叉路口遇到红灯,相当于独立重复试验,∴恰好遇到3次红灯概率为 ……………………………………………………(6分)
……………………………………………………(6分)
(2)记“经过交叉路口遇到红灯”事件为A,张华在第1、2个交叉路口未遇到红灯,在第3个交叉路口遇到红灯的概率为:
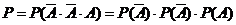
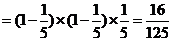 ………………………………………………………(12分)
………………………………………………………(12分)
17.解:(1)∵
∴
又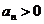 ,∴
,∴ ……………………………………………………2分
……………………………………………………2分
又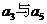 的等比中项为2,∴
的等比中项为2,∴
而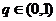 ,∴
,∴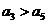 ,∴
,∴ ,
, …………………………………4分
…………………………………4分
∴ ,
,
∴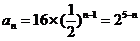 ………………………………………………………6分
………………………………………………………6分
(2) ……………………………………………………8分
……………………………………………………8分
由 ∴
∴
∴ 或
或 ………………………………………………………………10分
………………………………………………………………10分
故 ………………………………………………………12分
………………………………………………………12分
18.(1)解:由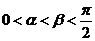 得
得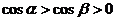
∵


∴
∴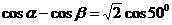
∴ ∴
∴
 ∴
∴ ……………………………………………8分
……………………………………………8分
(2)

 ……………………12分
……………………12分

19.解法一(几何法)
(1)证明:∵E是CD中点
∴ED=AD=1
∴∠AED=45°
同理∠CEB=45°
∴∠BEA=90° ∴EB⊥EA
∵平面D1AE⊥平面ABCE
∴EB⊥平面D1AE,AD1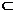 平面D1AE
平面D1AE
∴EB⊥AD1……4分
(2)设O是AE中点,连结OD1,因为平面
过O作OF⊥AB于F点,连结D
在Rt△D1OF中,D1O= ,OF=
,OF=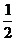
∴
∴ ,即二面角D1-AB-E等于
,即二面角D1-AB-E等于 ………………………9分
………………………9分
(3)延长FO交CD于G,过G作GH⊥D
∵AB⊥平面D1FG ∴GH⊥平面D1BA,
∵CE//AB ∴CE//平面D1BA.
∴C到平面D1BA的距离等于GH.
又D
∵FG・D1O=D
∴GH= 即点
即点 ………………………13分
………………………13分
另解:在Rt△BED1中,BD1= . 又AD1=1,AB=2
. 又AD1=1,AB=2
∴ ∴∠BD
∴∠BD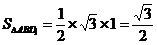
设点C到平面ABD1的距离为h 则
∴
∴ …………………………………13分
…………………………………13分
解法二:(向量法)
(1)证明:取AE的中点O,AB的中点F,连结D1O、OF,则OF//BE。
∵ DE=DA=1 ∴∠AED=45°
同理∠BEC=45° ∴∠BEA=90° ∴BE⊥EA ∴OF⊥AE
由已知D1O⊥EA
 又平面O1AE⊥平面ABCE,∴D1O⊥平面ABCE,以O为坐标原点,OF、OA、OD1所在直线分别为x、y、z轴,建立空间直角坐标系。则B(
又平面O1AE⊥平面ABCE,∴D1O⊥平面ABCE,以O为坐标原点,OF、OA、OD1所在直线分别为x、y、z轴,建立空间直角坐标系。则B( ),E(
),E( ),D1(
),D1( ),A(
),A( ),C(
),C( )
)
∴ ・
・ =(
=( )・(
)・( )=0
)=0
∴  ………………………………………………4分
………………………………………………4分
(2)解:设平面ABD1的一个法向量为
则
令 ,则y=1,z=1
,则y=1,z=1
∴  …………………………………………………………………6分
…………………………………………………………………6分
∵ OD1⊥平面ABCE.
∴ 是平面ABE的一个法向量.
是平面ABE的一个法向量.

∴ 即二面角D1-AB-E等于
即二面角D1-AB-E等于 . ………………………9分
. ………………………9分
(3)设点C到平面ABD1的距离为d,
则 ……………………………………………………………13分
……………………………………………………………13分
20.解:(1)因为 在区间(
在区间(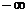 ,-2]上单调递增,在区间[-2,2]上单调递减,所以方程f′(x)
,-2]上单调递增,在区间[-2,2]上单调递减,所以方程f′(x) 的两根满足
的两根满足 ,
, …………2分
…………2分
由 ,得
,得 ,所以
,所以 ,而
,而 ,故b=0………………4分
,故b=0………………4分
则 ,从而
,从而
故 ……………………………………………………………………6分
……………………………………………………………………6分
(2)对任意的t1,t2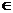 [m-2,m],不等式
[m-2,m],不等式 恒成立,等价于在区间[m-2,m]上,
恒成立,等价于在区间[m-2,m]上,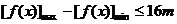 当0<m
当0<m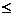 2时,[m-2,m]
2时,[m-2,m]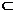 [ -2,2],所以
[ -2,2],所以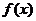 在区间[m-2,m]上单调递减,
在区间[m-2,m]上单调递减,
∴ ,
,  ……………………………………………9分
……………………………………………9分

解得 ……………………………………………………………………11分
……………………………………………………………………11分
又 ,∴
,∴ ,∴m的最小值是
,∴m的最小值是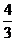 ……………………………………13分
……………………………………13分
21.解:(1)当AC垂直于x轴时, 由椭圆定义,有
由椭圆定义,有
∴ ,
, ………………………………………………………………2分
………………………………………………………………2分
在Rt△AF
∴ ∴
∴ ∴
∴ …………………………………………4分
…………………………………………4分
(2)由 得:
得: ∴
∴
∴ ∴
∴ ∴椭圆方程为
∴椭圆方程为
即 设
设 ,
, ,
,
(i)若直线AC的斜率存在,则直线AC方程为
∴ 代入椭圆方程有:
代入椭圆方程有:

∵ ∴
∴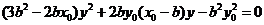
由韦达定理得: 所以
所以 ………………………8分
………………………8分
于是 同理可得:
同理可得: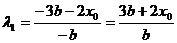
故 ……………………………………………………………………12分
……………………………………………………………………12分
(ii)若直线AC⊥x轴, ,
, ,
,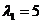 ,这时
,这时 ,
,
综上可知, 是定值6 …………………………………………………………13分
是定值6 …………………………………………………………13分

