1.已知集合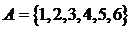 ,
,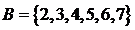 ,则集合
,则集合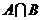 的真子集个数为 ( )
的真子集个数为 ( )
A 32个 B 31个 C 64个 D 63个
2.已知条件p: 内是增函数,条件q:
内是增函数,条件q: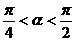 ,则p是q成立的( )
,则p是q成立的( )
A 充要条件 B 充分不必要条件
C 必要不充分条件 D 既不充分又不必要条件
3.若把函数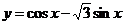 的图象沿向量
的图象沿向量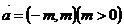 平移,使所得的图象关于
平移,使所得的图象关于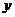 轴对称,则
轴对称,则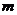 的最小值是
( )
的最小值是
( )
A 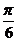 B
B 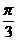 C
C 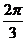 D
D 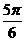
4.下列命题正确的是 ( )
A 垂直于同一平面的两个平面互相平行
B
经过平面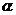 的一条斜线的平面
的一条斜线的平面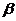 与平面
与平面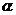 一定不垂直
一定不垂直
C 若a,b是异面直线,则过直线a一定不能作与直线b垂直的平面
D
若平面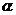 ,
,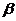 相交但不垂直,则平面
相交但不垂直,则平面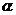 内任意一条直线都与平面
内任意一条直线都与平面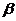 不垂直
不垂直
5.已知等差数列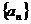 的前
的前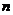 项和为
项和为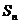 ,且
,且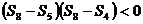 ,则
( )
,则
( )
A 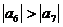 B
B 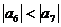 C
C 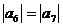 D
D 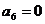
6.已知二项式(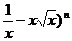 的展开式中含有
的展开式中含有 的项, 则n的一个可能值是
( )
的项, 则n的一个可能值是
( )
A 6 B
7.已知变量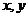 满足约束条件
满足约束条件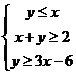 ,则目标函数
,则目标函数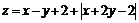 的最大值为( )
的最大值为( )
A 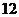 B
B
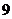 C
C
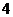 D
D 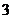
8.已知二面角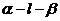 的平面角为
的平面角为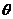 ,
,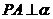 ,
, ,
,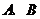 为垂足,设
为垂足,设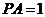 ,
,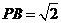 ,
,
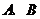 到棱
到棱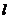 的距离分别为
的距离分别为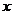 、
、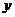 ,当
,当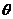 变化时,点
变化时,点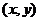 的轨迹是
( )
的轨迹是
( )
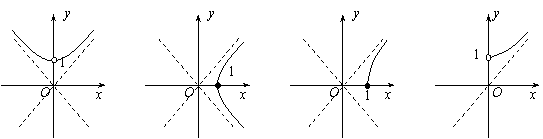 |
A B C D
9.已知函数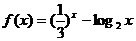 ,正实数a、b、c成公差为正数的等差数列,且满足
,正实数a、b、c成公差为正数的等差数列,且满足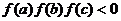 ,若实数d 是方程
,若实数d 是方程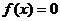 的一个解,那么下列四个判断:①
的一个解,那么下列四个判断:①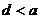 ;②
;②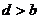 ;③
;③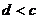 ;④
;④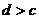 中有可能成立的个数为 ( )
中有可能成立的个数为 ( )
A 1 B
10.已知实数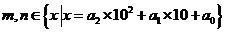 ,其中
,其中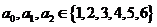 ,且
,且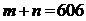 ,则实数对
,则实数对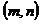 表示平面上不同点的个数为
( )
表示平面上不同点的个数为
( )
A 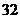 个
B
个
B
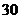 个
C
个
C
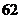 个
D
个
D
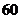 个
个
11.将一组样本数据中的每一个数据都乘以2,再都减去80,得到一组新的样本数据. 若求得新的样本数据的平均数是1.2,方差是4.4,则原样本数据的平均数为 ▲ ,方差为 ▲ 。
12.已知函数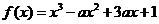 在区间
在区间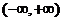 内存在极值,则实数
内存在极值,则实数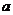 的取值范围为 ▲ 。
的取值范围为 ▲ 。
13.已知平面内的向量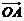 、
、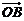 满足:|
满足:|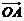 |=|
|=|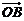 |=1,
|=1, 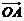 与
与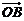 的夹角为
的夹角为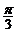 ,又
,又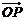 =x
=x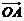 +y
+y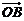 ,
,

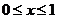 ,
,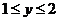 ,则点
,则点 的集合所表示的图形面积为 ▲ 。
的集合所表示的图形面积为 ▲ 。
14.已知椭圆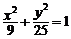 上的点
上的点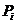 与
与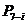 (i=1,2,3)关于x轴对称,且
(i=1,2,3)关于x轴对称,且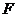 为该椭圆的一个焦点,则
为该椭圆的一个焦点,则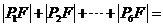 ▲ 。
▲ 。
15.如图为类似课本研究性学习课题《杨辉三角》中的竖直平面内一些通道,
图中粗线条均表示通道,一钢珠从入口处自上而下沿通道自由落入乙处
的概率是 ▲ 。 (第15题图)
16.已知直线 相切,其中m、
相切,其中m、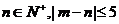 ,试写出所有满足条件的有序实数对(m,n): ▲ 。
,试写出所有满足条件的有序实数对(m,n): ▲ 。
17.(本小题满分12分)
已知△ABC的面积为 ,且满足
,且满足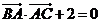 。
。
(Ⅰ)求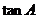 的值;
的值;
(Ⅱ)求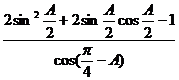 的值。
的值。
18.(本小题满分14分)
已知椭圆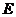 :
: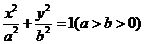 的左、右焦点分别为
的左、右焦点分别为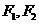 ,
, 为椭圆
为椭圆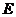 上的任意一点,满足
上的任意一点,满足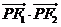 的最小值为
的最小值为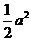 ,过
,过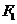 作垂直于椭圆长轴的弦长为3.
作垂直于椭圆长轴的弦长为3.
(Ⅰ)求椭圆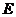 的方程;
的方程;
(Ⅱ)若过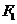 的直线交椭圆于
的直线交椭圆于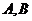 两点,求
两点,求 的取值范围.
的取值范围.
19.(本小题满分14分)
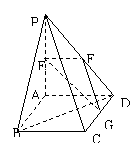 如图,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点。
如图,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点。
|

 ,函数
,函数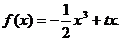
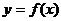 在区间[0,2]的最值;
在区间[0,2]的最值; 在区间[-2,2]上是单调函数,求t的取值范围;
在区间[-2,2]上是单调函数,求t的取值范围;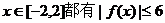 恒成立,若存在,请求出t,若不存在请说明理由.
恒成立,若存在,请求出t,若不存在请说明理由.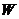 是满足下列两个条件的无穷数列
是满足下列两个条件的无穷数列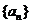 的集合:
的集合: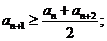 ②
②
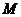 是与
是与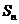 是其前n项的和,
是其前n项的和, ,证明:
,证明: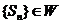 ;
;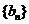 的通项为
的通项为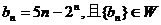 ,求
,求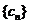 的各项均为正整数,且
的各项均为正整数,且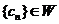 ,试证
,试证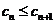 。
。