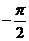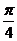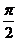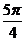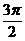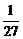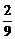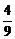∴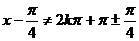 ,得x≠2kp
+p,且
,得x≠2kp
+p,且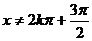 ,k∈Z
,k∈Z
∴函数f(x)的定义域为{x| x∈R,且x≠2kp
+p,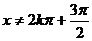 ,k∈Z }.………………………3分
,k∈Z }.………………………3分
又 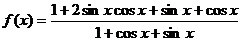
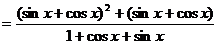
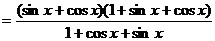 =
=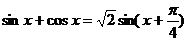 ,
,
所以,函数f(x)的周期是2p.……………………………………………………………………8分
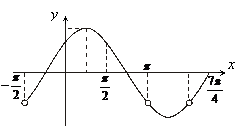 (Ⅱ)在
(Ⅱ)在 上取值列表为:
上取值列表为:
x
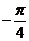
0
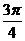
p
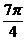
f (x)
不存在
0
1

1
0
不存在
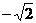
不存在
0
……………………………………………………………………………………………………………12分
18.由题意知,x 的取值为-6,-3,0,3.
∵ 珠子是等可能地随机滚入三个盒子中,∴
珠子滚入每个盒子的概率都是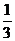 .………………3分
.………………3分
∴ P(x =-6)=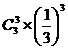 =
=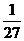 ,P(x =-3)= 2×
,P(x =-3)= 2×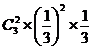 =
=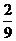 ,
,
P(x = 0)=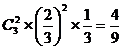 ,P(x = 3)=
,P(x = 3)=
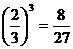 .…………………………………………9分
.…………………………………………9分
x
-6
-3
0
3
P

∴ x 的分布列是:
………………………………10分
x 的数学期望 Ex =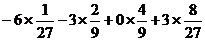 = 0.……………………………………………12分
= 0.……………………………………………12分
19.(Ⅰ)取A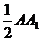 .∵ ABC-A1B
.∵ ABC-A1B
∴ B1E∥AA1,而E是BB1的中点,∴ B1E =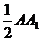 ,∴ DF∥B1E 且 DF = B1E,
,∴ DF∥B1E 且 DF = B1E,
∴ 四边形DEB
所以 DE∥平面A1B
(Ⅱ)假设存在点E使平面EAC1⊥平面ACC
∴ EM⊥平面ACC
由B1B∥平面ACC
 ∴
四边形EMNB是平行四边形,得 MN∥BE,且MN = BE,MN∥CC1.
∴
四边形EMNB是平行四边形,得 MN∥BE,且MN = BE,MN∥CC1.
 在△ABC中,cos∠BAC =
在△ABC中,cos∠BAC = ,
,
∴ ∠BAC = 45°.在Rt△ABN中,得 AN = 1.∵ MN∥CC1,
∴ 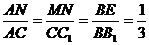 ,即在棱BB1上存在点E,
,即在棱BB1上存在点E,
当 时,二面角E?AC1?C是直二面角.……………………………12分
时,二面角E?AC1?C是直二面角.……………………………12分
(Ⅱ)如图所示建立空间直角坐标系.则三角形ABC的面积为
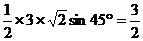 ,∴ 点A到BC所在直线的距离AD满足
,∴ 点A到BC所在直线的距离AD满足
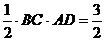 ,而BC =
,而BC =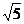 ,得
,得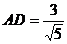 ,∴
,∴ .
.
设BE = m,BB1
= lm(m,l≠0),则 ,
,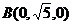 ,
, ,C1(0,0,lm).
,C1(0,0,lm).
在此坐标系下,很容易得到平面ACC .
.
 ,
, .
.
设平面EAC1的一个法向量为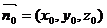 .
.
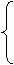
 = 0
= 0
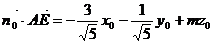 = 0
= 0
 即
即 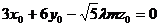 ,
,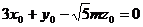 .
.
取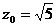 ,可得
,可得 ,
,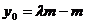 .
.
当二面角E?AC1?C是直二面角时,有 =
=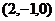 ・
・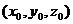 = 0,
= 0,
∴ 2( )-(lm-m)= 0,解得 l = 3,即在棱BB1上存在点E,当
)-(lm-m)= 0,解得 l = 3,即在棱BB1上存在点E,当 时,二面角E?AC1?C是直二面角.………………………………………………………………………………12分
时,二面角E?AC1?C是直二面角.………………………………………………………………………………12分
20.因为
f (x) =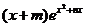 ,所以 f ′ (x) =
,所以 f ′ (x) =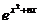 +
+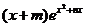 ( 2x + n )
( 2x + n )
= [ 2x2 +(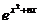 .………………………………………………………………3分
.………………………………………………………………3分
(Ⅰ)当m = 1,n = 5时,f ′ (x) =(2x2
+ 7x + 6)・ ,注意到
,注意到 >0,
>0,
则由f ′ (x)>0,解得 x<-2或x>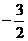 ;由f ′ (x)<0,解得-2<x<
;由f ′ (x)<0,解得-2<x<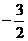 .
.
因此函数f (x) 在(-∞,-2)与(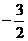 ,+∞)上递增;f (x) 在(-2,
,+∞)上递增;f (x) 在(-2,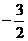 )上递减. ………6分
)上递减. ………6分
(Ⅱ)由已知有 f ′(0)= mn + 1,所以  =
= = f ′(0)= 4,
= f ′(0)= 4,
即 mn + 1 = 4,得 mn = 3.……………………………………………………………………………9分
要使函数f (x) =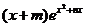 在R上单调递增,只须
f ′ (x)≥0在R上恒成立,
在R上单调递增,只须
f ′ (x)≥0在R上恒成立,
∴ 只须 ( 代入上式,
代入上式,
得( -n)2 ≤8,解得
-n)2 ≤8,解得  ≤n≤3
≤n≤3 .………………………………………………………………12分
.………………………………………………………………12分
21.(Ⅰ)由2 an+1 = 3an-an-1(n≥2),得 2(an+1-an)= an-an-1,
∴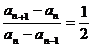 ,因此数列{ an-an-1
}是以a2-a1
= 1为首项,
,因此数列{ an-an-1
}是以a2-a1
= 1为首项, 为公比的等比数列,
为公比的等比数列,
∴ ,……………………………………………………………………………………4分
,……………………………………………………………………………………4分
于是 an =(an-an-1)+(an-1-an-2)+ … +(a2-a1)+ a1
= =
= .
………………………………………6分
.
………………………………………6分
(Ⅱ)由不等式 ,得
,得  ,
,
∴ 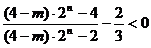 ,即
,即 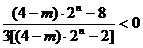 ,………………………………………………8分
,………………………………………………8分
所以 2<(4-m)・ 2n <8. ∵ 2n为正偶数,4-m为整数,
∴ (4-m)・ 2n = 4,或 (4-m)・ 2n = 6,
∴ 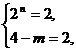 或
或 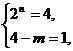 或
或 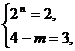 或
或 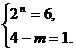
解得 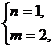 或
或 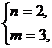 或
或 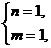 或
或 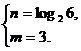
经检验使不等式 成立的所有正整数m、n的值为
成立的所有正整数m、n的值为
(m,n)=(1,1)或(2,1)或(3,2).………………………………………………………12分
说明 问题(1)的归纳做法是:由已知可得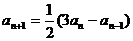 ,
,
∴  ,
,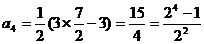 ,
,
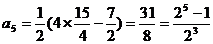 ,……,于是
,……,于是 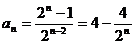 .
.
22.方法一:由题意知A(-a,0),F(c,0),a2
= b2 + c2, .
.
设点P的坐标为P(x0,y0),则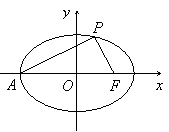
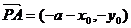 ,
,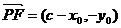 ,
,
∵ 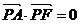 ,∴ PA⊥PF,表明△PAF是直角三角形,
,∴ PA⊥PF,表明△PAF是直角三角形,
于是 
∴ 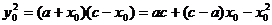 .(1)…………………………………………………4分
.(1)…………………………………………………4分
∵ P是椭圆C上在第一象限内的点,
∴ 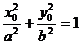 , 即
, 即  .(2) 将(1)代入(2)得
.(2) 将(1)代入(2)得 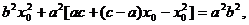
即 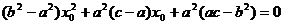 ,∴
,∴  ,
,
由于x0 + a>0,∴
只有 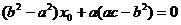 ,得
,得 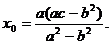 …………………………7分
…………………………7分
∵ c = ea,b2
= a2
? c2,∴ 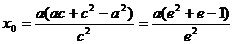 .(3)……………………………9分
.(3)……………………………9分
根据椭圆的定义,有 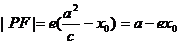 ,而
,而  ,
,
∴ 在Rt△PAF中,有 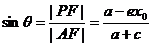 .(4) ……………………………………………11分
.(4) ……………………………………………11分
将(3)代入(4)得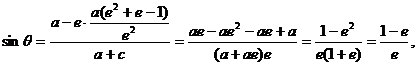 因此
因此  .…………………………………………………………………………………………14分
.…………………………………………………………………………………………14分
解法二 由题意知A(-a,0),F(c,0),a2
= b2 + c2, .
.
则直线PA的方程为 y =(x + a)tanq,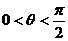 .(1)
.(1)
将直线PA的方程与椭圆方程联立,消去y后,得
(b2
+ a2 tan2q)x2 +
因为点A(-a,0)和P(x0,y0)的坐标满足方程(1)和(2),
所以,有 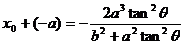 ,即
,即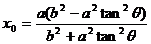 ,
,
y0 =(x0 + a)tanq
=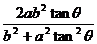 .……………………………………………………………………6分
.……………………………………………………………………6分
若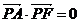 ,则PA⊥PF,表明△PAF是直角三角形,从而有 ?PA?2
+?PF?2
=?AF?2,
,则PA⊥PF,表明△PAF是直角三角形,从而有 ?PA?2
+?PF?2
=?AF?2,
∴ (x0 + a)2 + y02 +(x0-c)2 + y02 =(a + c)2,∴ x0 2 + y02 +(a-c)x0 = ac.……………8分
将x0、y0代入上式,得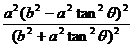 +
+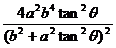 +
+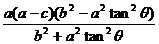 = ac.去分母,整理,得
= ac.去分母,整理,得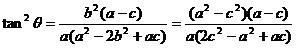 =
=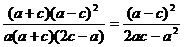 ,……………12分
,……………12分
将 c = ea代入,得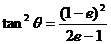 Û
Û
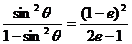 Û
Û
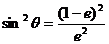 ,
,
于是 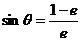 ,
, 为所求.…………………………………………………………14分
为所求.…………………………………………………………14分