1.在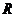 上,函数
上,函数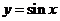 与函数
与函数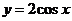 具有
具有
A.相同的单调性 B.相同的周期性 C.相同的奇偶性 D.相同的值域
2.某校现有高一学生210人,高二学生270人,高三学生300人,学校学生会用分层抽样的方法从这三个年级的学生中随机抽取n名学生进行问卷调查,如果已知从高一学生中抽取的人数为7,那从高三学生中抽取的人数应为
A.10 B.9 C.8 D.7
3.已知集合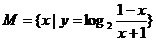 ,
,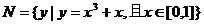 ,
,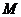 ∩
∩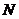 =
=
A.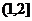 B.
B.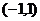 C.
C.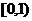 D.
D.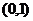
4.已知两圆方程分别为: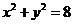 ,
,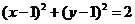 ,则两圆的公切线方程为
,则两圆的公切线方程为
A.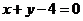 B.
B.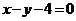 C.
C.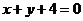 D.
D.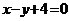
5.数列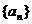 (
(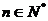 )中,
)中,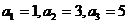 ,且
,且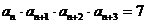 ,则
,则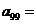
A.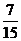 B.1 C.3
D.5
B.1 C.3
D.5
6.已知平面上不同的四点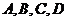 ,若
,若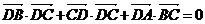 ,则
,则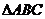 是
是
A.等腰三角形 B.等边三角形 C.直角三角形 D.任意三角形
7.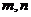 是异面直线,
是异面直线,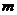 ⊥平面
⊥平面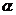 ,
,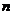 ⊥平面
⊥平面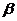 ,
,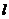 是直线,已知下列命题:
是直线,已知下列命题:
①若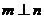 ,则
,则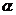 ⊥
⊥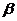 ②若
②若 ,则
,则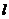 //
//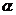 ,或
,或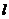 //
//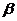
③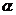 与
与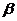 不可能平行; ④若
不可能平行; ④若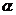 ⊥
⊥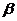 ,且
,且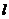 //
//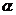 ,
,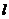 //
//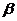 ,则
,则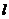 是
是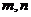 的公垂线
的公垂线
其中正确的命题是
A.①③ B.②④ C.①④ D.②③
8.在6张卡片上分别写有1,2,3,4,5,6,将它们排成一排,得到能被4整除的6位数共有
A.144个 B.120个 C.192个 D.168个
9.已知点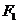 、
、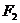 为双曲线
为双曲线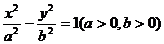 的左、右焦点,
的左、右焦点,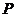 为右支上一点,点
为右支上一点,点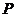 到右准线的距离为
到右准线的距离为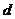 ,若
,若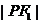 、
、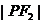 、
、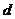 依次成等差数列,则此双曲线离心率取值范围是
依次成等差数列,则此双曲线离心率取值范围是
A.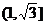 B.
B.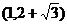 C.
C.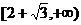 D.
D.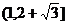
10.若函数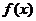 的导函数为
的导函数为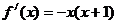 ,则函数
,则函数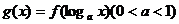 的单调递减区间是
的单调递减区间是
A.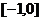 B.
B.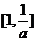 C.
C.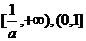 D.
D.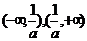
11.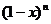 的展开式中
的展开式中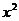 的系数是21,则
的系数是21,则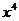 的系数为
.
的系数为
.
12.已知不等式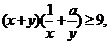 对任意正实数
对任意正实数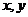 恒成立,则正实数
恒成立,则正实数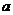 的最小值是 .
的最小值是 .
13.设函数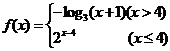 的反函数为
的反函数为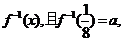
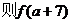 =
.
=
.
14.已知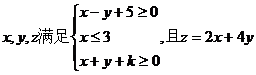 的最小值为
的最小值为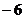 ,则常数
,则常数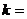 .
.
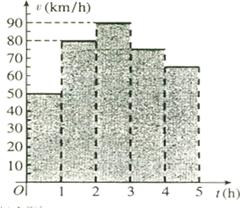 15.一辆汽车在某段路程中的行驶速度
15.一辆汽车在某段路程中的行驶速度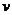 与时间
与时间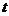
的关系如图所示,则(i)该汽车在前3小时内行驶的路程为 km;(ii)假设这辆汽车的里程表在汽车行驶这段路程前的读数为
km;(ii)假设这辆汽车的里程表在汽车行驶这段路程前的读数为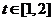 时,汽车里程表读数
时,汽车里程表读数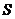 与时间
与时间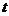 的函数解析式为
.
的函数解析式为
.
16.(本小题满分12分)通讯中,发报方常采取重复发送同一信号的办法来减少在接收中可能发生的错误.假定发报机只发0和1两种信号,接收时发生错误的情况是:“发0收到
17.(本小题满分12分) 在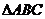 中,
中,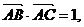
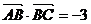 .(1)求AB边的长度;(2)求
.(1)求AB边的长度;(2)求 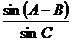 的值.
的值.
18.(本小题满分12分) 如图,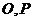 分别是正四棱柱
分别是正四棱柱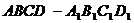 底面中心,
底面中心,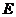 是
是
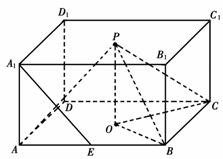
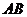 的中点,
的中点,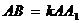 .
.
(1)求证: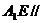 平面
平面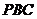 ;
;
(2)当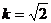 时,求直线
时,求直线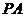 与平面
与平面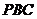
所成角的大小;
(3)当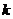 取何值时,
取何值时,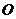 在平面
在平面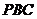 内的射影
内的射影
恰好为△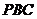 的重心?
的重心?
19.(本小题满分12分)已知数列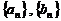 满足
满足 ,
,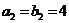 ,
,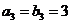 ,且
,且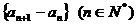 是等差数列,
是等差数列,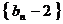
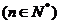 是等比数列.(1)求数列
是等比数列.(1)求数列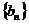 的通项公式;(2)求数列
的通项公式;(2)求数列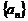 的通项公式;(3)是否存在
的通项公式;(3)是否存在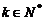 ,使
,使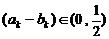 ?若存在,求出
?若存在,求出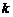 的值,;若不存在,说明理由.
的值,;若不存在,说明理由.
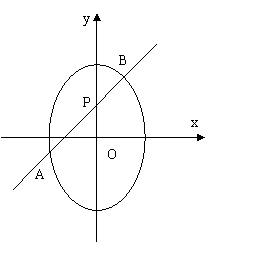 20.(本小题满分13分)椭圆
20.(本小题满分13分)椭圆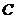 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在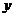 轴上,焦点到相应的准线的距离以及离心率均为
轴上,焦点到相应的准线的距离以及离心率均为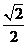 ,直线
,直线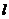 与
与
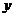 轴交于点
轴交于点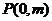 ,与椭圆
,与椭圆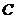 交于
交于
相异两点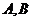 ,且
,且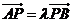 .
.
(1)求椭圆方程;
(2)若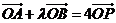 ,求
,求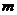 的
的
取值范围.
21.(本小题满分14分)已知函数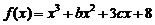 和
和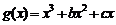 (其中
(其中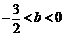 ),
),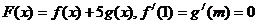 .(1)求
.(1)求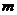 的取值范围;
的取值范围;
(2)方程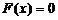 有几个实根?为什么?
有几个实根?为什么?
长沙市雅礼中学2007届高三月考试卷
数 学(文史类)答案
1.B 2.A 3.C 4.A 5.D
6.C 7.A 8.C 9.D 10.B
11.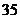
12.
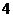
13.-2
14.
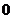
15.(i) ;(ii)
;(ii)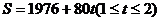
16.(本小题满分12分)
解:(1)正确接收一个信号的概率为
(1-0.05)×(1-0.05)=0.9025 …………………………………………………… 2分
错误接收一个信号的概率为0.05×0.05=0.0025 ……………………………… 4分
∴接收方接收一个信号的概率为0.9025+0.0025=0.905 …………………… 6分
(2)考虑对立事件,错误接收一个信号的概率为
23×0.052×0.95+33×0.053=0.00725
∴正确接收一个信号的概率为1-0.00725=0.99275. …………………………12分
17.(本小题满分12分)
解:(1)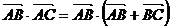
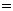
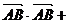
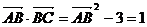 .
.
∴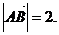 即AB边的长度为2.………………………………………………………5分
即AB边的长度为2.………………………………………………………5分
另解:用数量积的定义结合余弦定理即得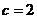 .
.
(2)由已知及(1)有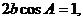
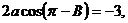
∴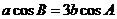 , ………………………………………………………………8分
, ………………………………………………………………8分
由正弦定理得: 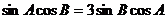 , ………………………………………10分
, ………………………………………10分
∴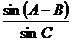 =
=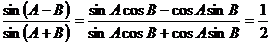 . ……………………12分
. ……………………12分
18.(本小题满分12分)
解:(1)过P作MN∥B
∵E、M分别为AB、A1B1中点,∴A1E∥MB
又MB⊂平面PBC,∴A1E∥平面PBC. ……………………………………………4分
(2)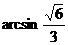 . ……………………………………………………………………8分
. ……………………………………………………………………8分
(3)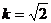 . ………………………………………………………………………12分
. ………………………………………………………………………12分
19.(本小题满分12分)
解:(1)∵{bn-2} (nÎZ+)为等比数列,又b1-2=4,b2-2=2,b3-2=1,
\公比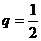 ,
,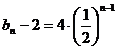 ,
,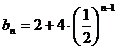 (nÎZ+) . ……………… 4分
(nÎZ+) . ……………… 4分
(2)∵{an+1-an} (nÎZ+)是等差数列,又a2-a1=-2,a3-a2=-1,\公差d=1,
an+1-an=-2+(n-1)=n-3,于是
an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=[(n-1)-3]+[(n-2)-3]+…+(1-3)+6
=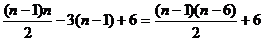 (nÎZ+). ……………………………
8分
(nÎZ+). ……………………………
8分
(3)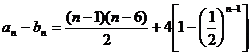 ,∵
,∵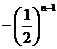 随正整数n的增加而增加
随正整数n的增加而增加
\当n³6时, ,
,
又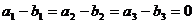 ,
, 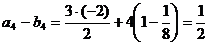 ,
,
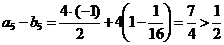 ,
,
由此可见,不存在kÎZ+,使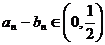 .………………………………………12分
.………………………………………12分
20.(本小题满分13分)
解:(1)设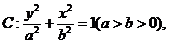 设
设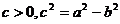 ,由条件知
,由条件知
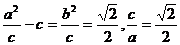 ,
,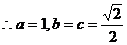 ,
,
故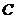 的方程为:
的方程为: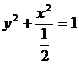 . ……………………………………………………4分
. ……………………………………………………4分
(2)由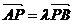 得
得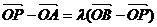
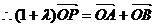 ,
,
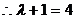 ,
, 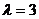 . ……………………………………………………………6分
. ……………………………………………………………6分
(另解:向量坐标化也可以得到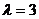 )
)
设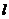 与椭圆
与椭圆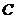 交点为
交点为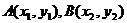
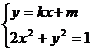 得
得
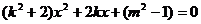 ,
,
当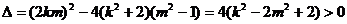 时,
时,
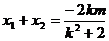 ,
,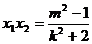 . ………………………………………………8分
. ………………………………………………8分
因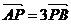 即
即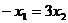 ,故
,故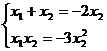 消
消 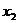 得
得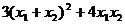 =0,
=0,
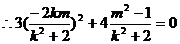 ,整理得
,整理得 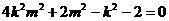 . …………10分
. …………10分
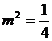 时,上式不成立;所以
时,上式不成立;所以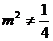 ,得
,得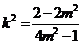 ,因
,因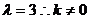
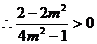 ,
,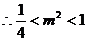 ,即
,即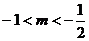 或
或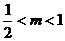 ,
,
即所求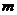 的取值范围为
的取值范围为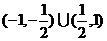 . …………………………………………13分
. …………………………………………13分
21.(本小题满分14分)
解:(1)∵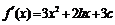 ,
,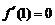 ,∴
,∴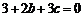 ,∴
,∴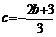 . …………1分
. …………1分
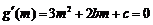 ,即
,即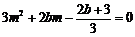 ,∴
,∴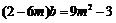 .……3分
.……3分
①当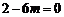 ,即
,即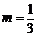 时,上式不成立. …………………………………………4分
时,上式不成立. …………………………………………4分
②当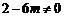 ,即
,即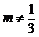 时,
时,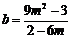 .由条件
.由条件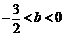 ,得到
,得到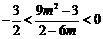 .
.
由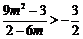 ,解得
,解得 或
或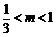 . ……………………………………………5分
. ……………………………………………5分
由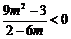 ,解得
,解得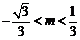 或
或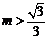 . ………………………………………6分
. ………………………………………6分
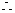 m的取值范围是
m的取值范围是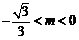 或
或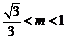 .………………………………………7分
.………………………………………7分
(2)有一个实根. ………………………………………………………………………8分
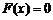 ,即
,即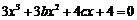 .记
.记 ,
,
则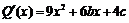 .∵
.∵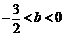 ,
,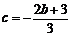
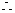
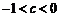 .………………10分
.………………10分
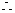 △>0,故
△>0,故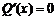 有相异两实根
有相异两实根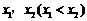 .
.
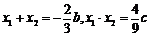 ,∴
,∴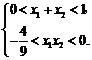 显然
显然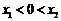 ,
,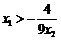 ,
,
∴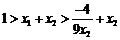 ,∴
,∴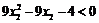 ,∴
,∴ . ………………………12分
. ………………………12分
于是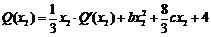
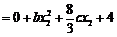
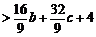
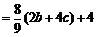
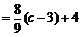
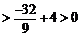 .
.
而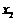 为三次函数
为三次函数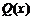 的极小值点,故
的极小值点,故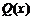 与x轴只有一个交点.
与x轴只有一个交点.
∴ 方程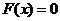 只有一个实根.……………………………………………………14分
只有一个实根.……………………………………………………14分

