1、函数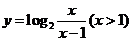 的反函数是
的反函数是
A.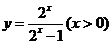 B.
B.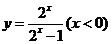 C.
C.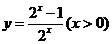 D.
D.
2、函数 的定义域是
的定义域是
A.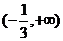 B.
B. 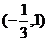 C.
C. 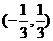 D.
D.
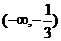
3、下列函数中,在其定义域内既是奇函数又是减函数的是
A. 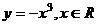 B.
B. 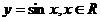 C.
C. 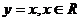 D.
D. 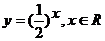
4、已知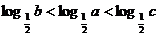 ,则
,则
A. 2b>
5、设函数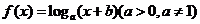 的图像过点
的图像过点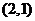 ,其反函数的图像过点
,其反函数的图像过点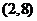 ,则
,则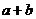 等于
等于
A.3 B
6、设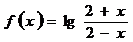 ,则
,则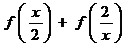 的定义域为
的定义域为
A. 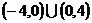 B.
B. 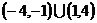 C.
C. 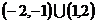 D.
D. 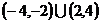
7、若函数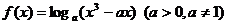 在区间
在区间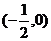 内单调递增,则a的取值范围是
内单调递增,则a的取值范围是
A.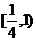 B.
B. 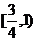 C.
C.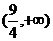 D.
D.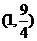
8、为确保信息安全,信息需加密传输,发送方由明文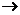 密文(加密),接收方由密文
密文(加密),接收方由密文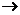 明文(解密),已知加密规则为:明文
明文(解密),已知加密规则为:明文 对应密文
对应密文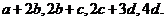 例如,明文
例如,明文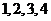 对应密文
对应密文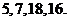 当接收方收到密文
当接收方收到密文 时,则解密得到的明文为A.
时,则解密得到的明文为A.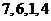 B.
B.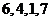 C.
C.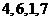 D.
D.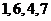
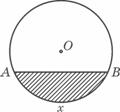 9、如图所示,单位圆中弧AB的长为x,f(x)表示弧AB与弦AB
9、如图所示,单位圆中弧AB的长为x,f(x)表示弧AB与弦AB
所围成的弓形面积的2倍,则函数y=f(x)的图象是
|

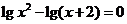 的解集是
的解集是
 对于任意实数
对于任意实数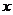 满足条件
满足条件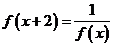 ,若
,若 则
则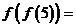 __________。
__________。
 是奇函数,则a=
.
是奇函数,则a=
.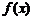 是定义在
是定义在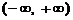 上的偶函数. 当
上的偶函数. 当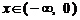 时,
时,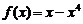 ,则当
,则当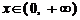 时,
时,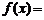
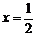 对称,则f (1)+ f (2)+ f (3)+ f (4)+ f
(5)=________________.
对称,则f (1)+ f (2)+ f (3)+ f (4)+ f
(5)=________________.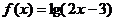 的定义域为集合M,函数
的定义域为集合M,函数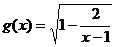 的定义域为集合N.求:
的定义域为集合N.求: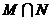 ,
,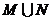 .
.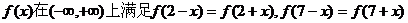 ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有
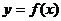 的奇偶性;
的奇偶性;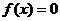 在闭区间[-2005,2005]上的根的个数,并证明你的结论.
在闭区间[-2005,2005]上的根的个数,并证明你的结论.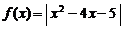 .
.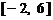 上画出函数
上画出函数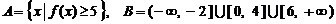 . 试判断集合
. 试判断集合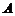 和
和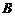 之间的关系,并给出证明;
之间的关系,并给出证明;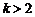 时,求证:在区间
时,求证:在区间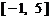 上,
上,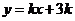 的图像位于函数
的图像位于函数
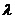 f(x)+1在[-1,1]上是增函数,求实数
f(x)+1在[-1,1]上是增函数,求实数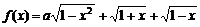 的最大值为g(a)。
的最大值为g(a)。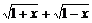 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)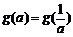 的所有实数a
的所有实数a 安宜高级中学2006-2007学年度第一学期
安宜高级中学2006-2007学年度第一学期 19题解:
19题解: