13、若正整数m满足
- 答案
ABAACBBCDB

 155
155

 0
0
17、解:(Ⅰ)
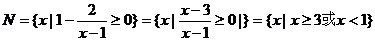
(Ⅱ)

18、解: (I) 由于在闭区间[0,7]上,只有 ,故
,故 .若
.若 是奇函数,则
是奇函数,则 ,矛盾.所以,
,矛盾.所以, 不是奇函数.
不是奇函数.
由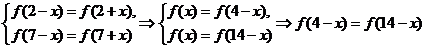
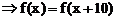 , 从而知函数
, 从而知函数 是以
是以 为周期的函数.
为周期的函数.
若 是偶函数,则
是偶函数,则 .又
.又 ,从而
,从而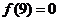 .
.
由于对任意的 (3,7]上,
(3,7]上, ,又函数
,又函数 的图象的关于
的图象的关于 对称,所以对区间[7,11)上的任意
对称,所以对区间[7,11)上的任意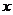 均有
均有 .所以,
.所以,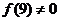 ,这与前面的结论矛盾.
,这与前面的结论矛盾.
所以,函数 是非奇非偶函数.
是非奇非偶函数.
(II) 由第(I)小题的解答,我们知道 在区间(0,10)有且只有两个解,并且
在区间(0,10)有且只有两个解,并且 .由于函数
.由于函数 是以
是以 为周期的函数,故
为周期的函数,故 .所以在区间[-2000,2000]上,方程
.所以在区间[-2000,2000]上,方程 共有
共有 个解.
个解.
在区间[2000,2010]上,方程 有且只有两个解.因为
有且只有两个解.因为
 ,
,
所以,在区间[2000,2005]上,方程 有且只有两个解.
有且只有两个解.
在区间[-2010,-2000]上,方程 有且只有两个解.因为
有且只有两个解.因为
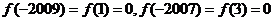 ,
,
所以,在区间[-2005,-2000]上,方程 无解.
无解.
综上所述,方程 在[-2005,2005]上共有802个解.
在[-2005,2005]上共有802个解.
 19、[解](1)
19、[解](1)
(2)方程 的解分别是
的解分别是 和
和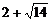 ,由于
,由于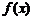 在
在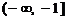 和
和 上单调递减,在
上单调递减,在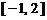 和
和 上单调递增,因此
上单调递增,因此
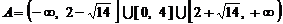 .
.
由于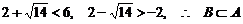 .
.
(3)[解法一] 当 时,
时, .
.
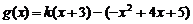
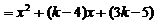
 ,
,

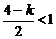 . 又
. 又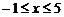 ,
,
①
当 ,即
,即 时,取
时,取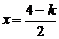 ,
,

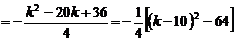 .
.
 ,
,
则 .
.
②
当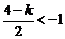 ,即
,即 时,取
时,取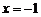 ,
,  =
= .
.
由 ①、②可知,当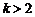 时,
时, ,
, .
.
因此,在区间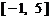 上,
上, 的图像位于函数
的图像位于函数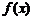 图像的上方.
图像的上方.
[解法二] 当 时,
时, .
.
由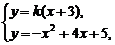 得
得 ,
,
令  ,解得
,解得  或
或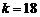 ,
,
在区间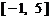 上,当
上,当 时,
时, 的图像与函数
的图像与函数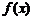 的图像只交于一点
的图像只交于一点 ; 当
; 当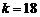 时,
时, 的图像与函数
的图像与函数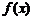 的图像没有交点.
的图像没有交点.
如图可知,由于直线 过点
过点 ,当
,当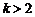 时,直线
时,直线 是由直线
是由直线 绕点
绕点 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间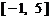 上,
上, 的图像位于函数
的图像位于函数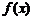 图像的上方.
图像的上方.
20、解:(Ⅰ)设函数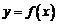 的图象上任意一点
的图象上任意一点 关于原点的对称点为
关于原点的对称点为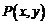 ,则
,则
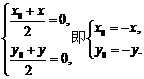
∵点 在函数
在函数 的图象上
的图象上
∴
(Ⅱ)由
当 时,
时, ,此时不等式无解
,此时不等式无解
当 时,
时, ,解得
,解得

因此,原不等式的解集为

(Ⅲ)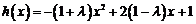
①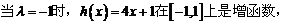

②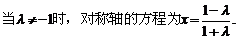
?)
?)

21、解:(I)∵ ,
,
∴要使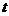 有意义,必须
有意义,必须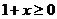 且
且 ,即
,即
∵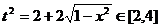 ,且
,且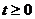 ……① ∴
……① ∴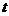 的取值范围是
的取值范围是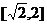 。
。
由①得: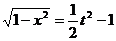 ,∴
,∴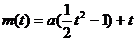
 ,
, 。
。
(II)由题意知 即为函数
即为函数
 ,
, 的最大值,
的最大值,
∵直线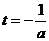 是抛物线
是抛物线
 的对称轴,∴可分以下几种情况进行讨论:
的对称轴,∴可分以下几种情况进行讨论:
(1)当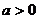 时,函数
时,函数 ,
, 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由 知
知 在
在 上单调递增,故
上单调递增,故

 ;
;
(2)当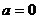 时,
时, ,
, ,有
,有 =2;
=2;
(3)当 时,,函数
时,,函数 ,
, 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若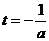
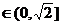 即
即 时,
时,
 ,
,
若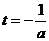
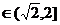 即
即 时,
时,
 ,
,
若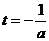
 即
即 时,
时,

 。
。
综上所述,有 =
= 。
。
(III)当 时,
时,

 ;
;
当 时,
时, ,
,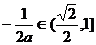 ,∴
,∴ ,
,

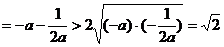 ,故当
,故当 时,
时,
 ;
;
当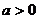 时,
时, ,由
,由
 知:
知:
 ,故
,故 ;
;
当 时,
时,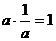 ,故
,故 或
或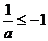 ,从而有
,从而有 或
或 ,
,
要使
 ,必须有
,必须有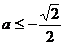 ,
, ,即
,即 ,
,
此时,
 。
。
综上所述,满足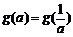 的所有实数a为:
的所有实数a为: 或
或 。
。

