1.在等差数列{an}中, a7=9, a13=-2, 则a25=
A.-22
B.-
2.在等比数列{an}中, 存在正整数m, 有am=3,am+5=24, 则am+15=
A.864
B.
3.已知等差数列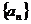 的公差为2,若
的公差为2,若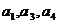 成等比数列, 则
成等比数列, 则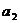 =
=
A.-4
B.-
4.设数列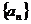 是等差数列,且
是等差数列,且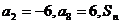 是数列
是数列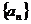 的前n项和,则
的前n项和,则
A.S4>S3 B.S4=S
5.已知由正数组成的等比数列{an}中,公比q=2, a1・a2・a3・…・a30=245, 则a1・a4・a7・…・a28=
A.25
B.
6.若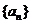 是等差数列,首项
是等差数列,首项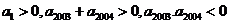 ,则使前n项和
,则使前n项和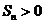 成立的最大自然数n是
成立的最大自然数n是
A.4005
B.
7.在等比数列{an}中, a1<0, 若对正整数n都有an<an+1, 那么公比q的取值范围是
A.q>1
B.0<q<
8.已知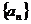 为等差数列,公差
为等差数列,公差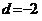 ,
,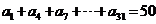 ,则
,则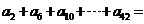
A.60
B.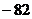 C.182
D.
C.182
D.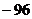
9.已知等比数列{an} 的前n项和为Sn , 若S4=1,S8=4,则a13+a14+a15+a16=
A.7
B.
10.数列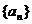 的前
的前 项和为
项和为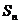 ,若
,若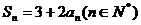 ,则这个数列一定是
,则这个数列一定是
A.等比数列 B.等差数列
C.从第二项起是等比数列 D.从第二项起是等差数列
11.等差数列{an}中,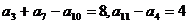 .记
.记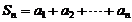 ,则S13等于
,则S13等于
A.168
B.
12.设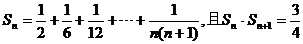 ,则
,则 的值为
的值为
A.9
B.
13.设等比数列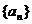 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为_________________.
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为_________________.
14.数列1,1+2,1+2+22,……,1+2+22+……+2n-1,……的前n项和是Sn=_________
15.等差数列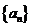 前
前 项和为
项和为 ,已知
,已知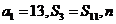 为________时,
为________时, 最大.
最大.
16.已知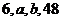 成等差数列,
成等差数列, 成等比数列,则
成等比数列,则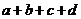 的值为_________.
的值为_________.
17.(本小题满分12分)
已知数列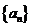 满足
满足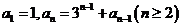 .
.
(1)求 ;
;
(2)证明: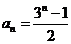 .
.
18.(本小题满分12分)
有固定项的数列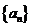 的前
的前 项和
项和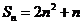 ,现从中抽取某一项(不包括首相、末项)后,余下的项的平均值是79.
,现从中抽取某一项(不包括首相、末项)后,余下的项的平均值是79.
(1)求数列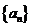 的通项
的通项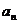 ;
;
(2)求这个数列的项数,抽取的是第几项?
19.(本小题满分12分)
设实数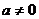 ,数列
,数列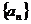 是首项为
是首项为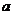 ,公比为
,公比为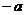 的等比数列,记
的等比数列,记
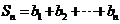 ,
,
求证:当 时,对任意自然数
时,对任意自然数 都有
都有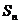 =
=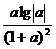
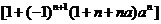
20.(本小题满分12分)
在公差为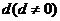 的等差数列
的等差数列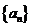 和公比为
和公比为 的等比数列
的等比数列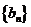 中,已知
中,已知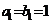 ,
, ,
,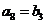 .
.
(1)求数列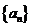 与
与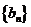 的通项公式;
的通项公式;
(2)是否存在常数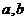 ,使得对于一切正整数
,使得对于一切正整数 ,都有
,都有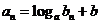 成立?若存在,求出常数
成立?若存在,求出常数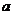 和
和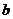 ,若不存在,说明理由.
,若不存在,说明理由.
21.(本小题12分)
从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业.根据规划,本年度投入800万元,以后每年投入将比上年减少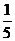 .本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
.本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加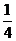 。
。
(1)设n年内(本年度为第一年)总投入为an万元,旅游业总收入为bn万元.写出an,bn的表达式
(2)至少经过几年旅游业的总收入才能超过总投入?
22.(本小题满分14分)
(文科做)设无穷等差数列{an}的前n项和为Sn.
(1)若首项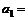 ,公差
,公差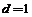 ,求满足
,求满足 的正整数k;
的正整数k;
(2)求所有的无穷等差数列{an},使得对于一切正整数k都有 成立.
成立.
(理科做)已知函数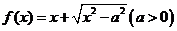 .
.
(1)求函数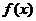 的反函数
的反函数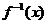 及其定义域;
及其定义域;
(2)数列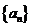 满足
满足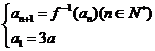 ,设
,设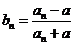 ,数列
,数列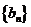 的前
的前 项和为
项和为 ,试比较
,试比较 与
与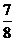 的大小,并证明你的结论.
的大小,并证明你的结论.

