13.A、B两质点的质量分别为
14.等轴双曲线xy = k(k为非零常数)的渐近线方程为______________.
15.已知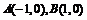 ,点
,点 满足
满足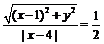 ,则
,则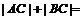 _________.
_________.
16.在椭圆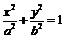 中
中 ,
,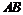 为过左焦点
为过左焦点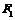 的弦,且
的弦,且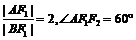 ,则椭圆的离心率
,则椭圆的离心率 ____________.
____________.
17.双曲线 左右顶点为
左右顶点为 ,
,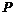 为右支上一点,且
为右支上一点,且 ,则
,则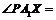 __________度.
__________度.
18.关于曲线C: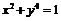 的下列说法:⑴关于点(0,0)对称,⑵关于直线
的下列说法:⑴关于点(0,0)对称,⑵关于直线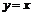 对称,⑶是封闭图形,面积小于
对称,⑶是封闭图形,面积小于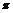 ,⑷是封闭图形,面积大于
,⑷是封闭图形,面积大于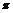 ,⑸不是封闭图形,无面积可言,其中正确的序号是_________________.
,⑸不是封闭图形,无面积可言,其中正确的序号是_________________.
19.直线 是
是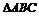 中
中 的平分线所在的直线,若
的平分线所在的直线,若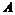 、
、 坐标分别为
坐标分别为 ,
,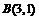 ,判断
,判断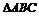 形状,并求面积.
形状,并求面积.
20.双曲线与椭圆在 轴上有公共焦点,若椭圆焦距为
轴上有公共焦点,若椭圆焦距为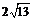 ,它们的离心率是方程
,它们的离心率是方程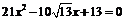 的两根,求双曲线和椭圆的标准方程.
的两根,求双曲线和椭圆的标准方程.
21.已知椭圆的中心在坐标原点,焦点在 轴上,它的一个焦点为
轴上,它的一个焦点为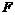 ,
,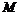 是椭圆上的任意点,
是椭圆上的任意点,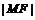 的最大值和最小值的积为4,椭圆上存在以
的最大值和最小值的积为4,椭圆上存在以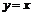 为轴的对称点
为轴的对称点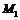 和
和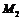 ,且
,且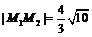 ,求椭圆的方程.
,求椭圆的方程.







 22.已知定点
22.已知定点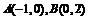 ,过点
,过点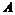 的直线
的直线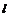 交半圆
交半圆 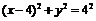
 ≥0
≥0 于P、Q两点,线段PQ中点为M,直线
于P、Q两点,线段PQ中点为M,直线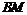 交
交 轴于
轴于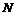 .
.
⑴若点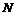 位于点
位于点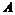 右侧,试求直线
右侧,试求直线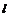 的斜率
的斜率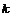 的取值范围.
的取值范围.
⑵若半圆的圆心为D,在⑴的条件下,△PDQ能否为正三角形?
23.椭圆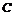 的中心在原点0,它的短轴长为
的中心在原点0,它的短轴长为 ,右焦点为
,右焦点为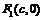 ,右准线
,右准线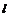 与
与 轴相交于点A,并且
轴相交于点A,并且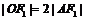 .
.
⑴求椭圆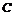 的方程.
的方程.
⑵过椭圆的左焦点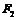 作一条与两坐标轴都不垂直的直线
作一条与两坐标轴都不垂直的直线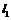 ,交椭圆于
,交椭圆于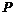 ,
,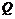 两点,若
两点,若 轴上的某一点
轴上的某一点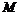 能使得
能使得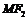 为
为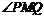 的平分线,则称点
的平分线,则称点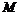 是椭圆的“左特征点”,求出此椭圆的“左特征点”
是椭圆的“左特征点”,求出此椭圆的“左特征点”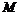 的坐标.
的坐标.
⑶请根据上面的结论猜想:椭圆 的“左特征点”
的“左特征点”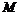 是怎样的点?并证明你的结论。
是怎样的点?并证明你的结论。
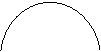
24.下面的图形既可看作是圆的一部分,也可以看作是椭圆的一部分,也可以看作是双曲线某一支的一部分,且只能是上述中的某一种你现有直尺、圆规和笔,你如何判断它们是上述曲线中的哪一类,写出判断的方法和依据.


