20.双曲线与椭圆在 轴上有公共焦点,若椭圆焦距为
轴上有公共焦点,若椭圆焦距为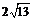 ,它们的离心率是方程
,它们的离心率是方程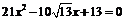 的两根,求双曲线和椭圆的标准方程.
的两根,求双曲线和椭圆的标准方程.
- 答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
C
C
A
C
B
C
C
B
B
C
二、填空题
13.(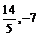 ) 14.x=0或y=0 15.4 16.2/3 17.20 18.①④
) 14.x=0或y=0 15.4 16.2/3 17.20 18.①④
三、解答题
19.解:A(―4,2)关于直线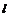 :
: 对称的点为
对称的点为 ,因为直线
,因为直线 是
是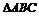 中
中 的平分线,可以点
的平分线,可以点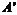 在直线
在直线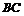 上,故直线
上,故直线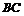 的方程是
的方程是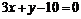 ,由
,由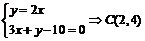 ,
,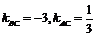 ,则
,则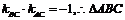 是以
是以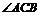 为直角的三角形,
为直角的三角形,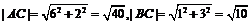 ,
,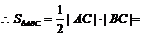 10
10
20.解:由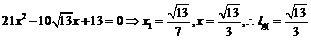 ,
,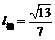 ,设双曲线方程为
,设双曲线方程为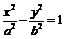 ,椭圆方程为
,椭圆方程为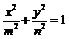 ,它们的焦点
,它们的焦点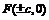 ,则
,则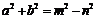
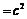
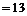 ,又
,又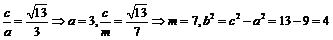 ,
,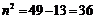 ,
,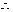 双曲线方程为
双曲线方程为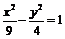 ,椭圆方程为
,椭圆方程为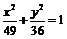
21.解: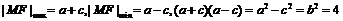 ,设椭圆方程为
,设椭圆方程为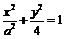 ①,设过
①,设过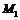 和
和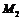 的直线方程为
的直线方程为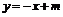 ②,将②代入①得
②,将②代入①得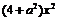 -
-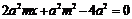 ③,设
③,设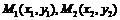 ,
,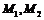 的中点为
的中点为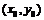
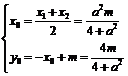 代入
代入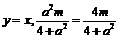 ,
,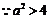 ,
,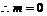 ,由③
,由③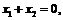
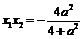 ,
,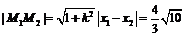 ,解得
,解得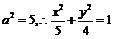
22.解:⑴设直线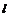 方程为:
方程为: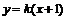 代入
代入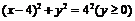 ,得
,得
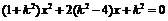 ,另知直线
,另知直线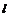 与半圆相交的条件为
与半圆相交的条件为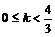 ,设
,设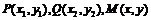 ,则
,则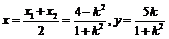 ,
,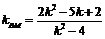 ,点
,点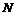 位于
位于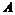 的右侧,应有
的右侧,应有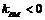 ,即
,即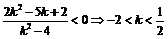 ,
,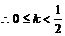 (亦可求出
(亦可求出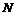 的横坐标
的横坐标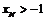 )
)
⑵若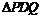 为正
为正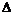 ,则点
,则点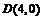 到直线
到直线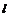 距离
距离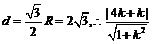
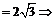
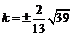 与
与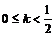 矛盾,
矛盾,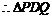 在⑴条件下不可能是正△.
在⑴条件下不可能是正△.
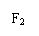 23.⑴由题意设椭圆方程为:
23.⑴由题意设椭圆方程为: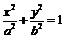 ,则
,则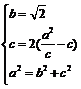 解得:
解得: 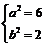 ,所以椭圆方程为:
,所以椭圆方程为: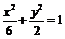
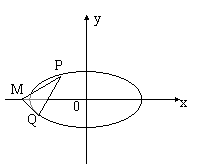
⑵设“左特征点”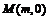 ,设
,设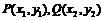 ,
,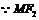 为
为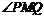 的平分线,
的平分线,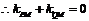 ,
,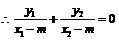 ,下面设直线
,下面设直线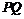 的方程为
的方程为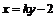 ,代入
,代入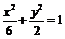 得:
得: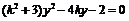 ,
,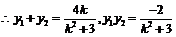 代入上式得
代入上式得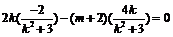 解得
解得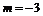
⑶椭圆 的“左特征点”M是椭圆的左准线和x轴的交点证明如下:
的“左特征点”M是椭圆的左准线和x轴的交点证明如下:
证明:设椭圆的左准线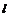 与x轴相交于点M,过点A、B分别作
与x轴相交于点M,过点A、B分别作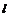 的垂线,垂足分别为点C、D。据椭圆第二定义得
的垂线,垂足分别为点C、D。据椭圆第二定义得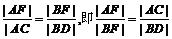 ,
,
∵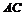 ∥
∥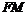 ∥
∥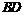 ,∴
,∴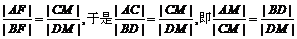 ,
,
∴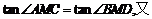 ∵
∵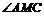 与
与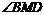 均为锐角,∴
均为锐角,∴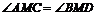 。
。
∴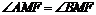 。∴
。∴ 为
为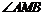 的平分线。故点
的平分线。故点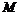 为椭圆的“左特征点”。
为椭圆的“左特征点”。

