1.设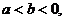 则下列不等式中
则下列不等式中 成立的是
成立的是
A. 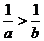 B.
B. 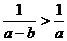 C.
C. 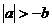 D.
D. 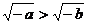
2.已知数列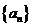 的通项公式
的通项公式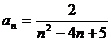 ,则
,则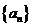 的最大项是
的最大项是
A.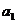 B.
B.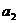 C.
C.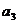 D.
D.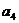
3.已知在△ABC中,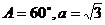 ,则
,则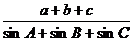 等于
等于
A.2 B.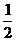 C.
C.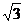 D.
D.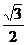
4.设实数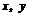 满足
满足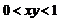 且
且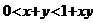 ,那么
,那么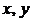 的取值范围是
的取值范围是
A.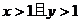 B.
B.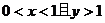
C.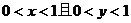 D.
D.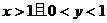
5.已知:在△ABC中,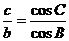 ,则此三角形为
,则此三角形为
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.正三角形
6.已知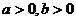 ,A是a、b的等差中项,G是a、b的等比中项,则
,A是a、b的等差中项,G是a、b的等比中项,则
A.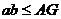 B.
B.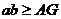 C.
C.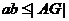 D.
D.
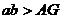
7.设等差数列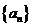 的前n项的和是Sn,且
的前n项的和是Sn,且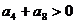 ,则
,则
A.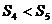 B.
B.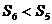 C.
C.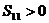 D.
D.
8.在R上定义运算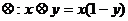 ,若不等式
,若不等式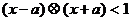 对任意实数
对任意实数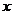 成立,则a的取值范围为
成立,则a的取值范围为
A.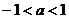 B.
B.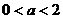 C.
C.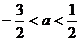 D.
D.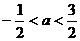
9.各项均为正数的等比数列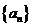 的公比
的公比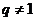 ,且
,且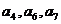 成等差数列,则
成等差数列,则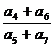 =
=
A.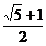 B.
B.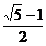 C.
C.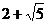 D.
D.
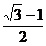
10.在△ABC中,已知AB=4,AC=7,BC边上的中线AD长为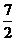 ,那么BC边的长为
,那么BC边的长为
A.7 B.
第Ⅱ卷(非选择题 共100分)
11.观察下列式子: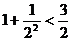 ,
, 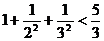 ,
,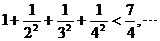 ;你可以猜想的结论为:
;你可以猜想的结论为: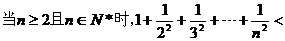 ▲
.
▲
.
12.若不等式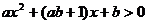 的解集是
的解集是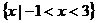 ,则
,则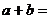 ▲ .
▲ .
13.随着计算机技术的不断发展,电脑的性能越来越好,而价格又在不断降低.若每隔两年电脑的价格可降低三分之一,则现在价格为8100元的电脑在6年后的价格可降为 ▲ 元.
14.已知函数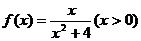 ,则函数图象上最高点的坐标为 ▲ .
,则函数图象上最高点的坐标为 ▲ .
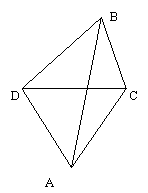 15.如图,我炮兵阵地位于A处,两观察所分别设于C,D,
15.如图,我炮兵阵地位于A处,两观察所分别设于C,D,
已知△ACD为边长等于a的正三角形, 当目标出现于B时,
测得∠CDB=45°∠BCD=75°,A、B、C、D在同一平面上,则炮击目标的距离AB= ▲ .(结果保留根式形式)
16.在数列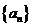 中,已知
中,已知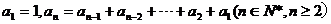 ,则这个数列的通项公式为
,则这个数列的通项公式为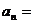 ▲
.
▲
.
17.(本小题满分12分)
已知函数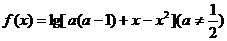 的定义域为集合A.
的定义域为集合A.
(1)若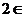 A,求
A,求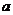 的取值范围;
的取值范围;
(2)求定义域集合A.
18.(本小题满分14分)
数列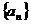 的前项
的前项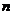 和记为
和记为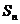 ,若数列
,若数列 是首项为9,公差为-1的等差数列.
是首项为9,公差为-1的等差数列.
(1)求数列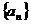 通项公式
通项公式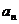 ;
;
(2)若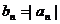 ,且数列
,且数列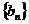 的前项
的前项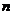 和记为
和记为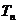 ,求
,求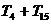 的值.
的值.
19.(本小题满分14分)
已知在△ABC中,三边长a,b,c依次成等差数列.
(1) 若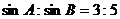 ,求三个内角中最大角的度数;
,求三个内角中最大角的度数;
(2)若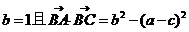 ,求△ABC的面积.
,求△ABC的面积.
20.(本小题满分15分)
已知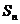 是首项为
是首项为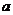 的等比数列
的等比数列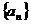 的前n项的和,
的前n项的和,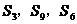 成等差数列,
成等差数列,
(1)求证: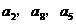 成等差数列;
成等差数列;
(2)若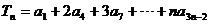 ,求
,求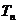
21.(本小题满分15分)
某外商到一开发区投资72万元建起一座蔬菜加工厂,第一年需各种经费为12万元,从第二年开始每年所需经费均比上一年增加4万元,该加工厂每年销售蔬菜总收入为50万元.
(I)若扣除投资及各种经费,该加工厂从第几年开始纯利润为正?
(II)若干年后,外商为开发新项目,对加工厂有两种处理方案:
(1)若年平均纯利润达到最大值时,便以48万元的价格出售该厂;
(2)若纯利润总和达到最大值时,便以16万元的价格出售该厂.
问:哪一种方案比较合算?请说明理由.
2005――2006学年(下)期中联考

