【题目】已知椭圆C: ![]() (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
参考答案:
【答案】(1)![]() .(2)见解析。
.(2)见解析。
【解析】试题分析:(1)根据![]() ,
, ![]() 两点关于y轴对称,由椭圆的对称性可知C经过
两点关于y轴对称,由椭圆的对称性可知C经过![]() ,
, ![]() 两点.另外由
两点.另外由![]() 知,C不经过点P1,所以点P2在C上.因此
知,C不经过点P1,所以点P2在C上.因此![]() 在椭圆上,代入其标准方程,即可求出C的方程;(2)先设直线P2A与直线P2B的斜率分别为k1,k2,再设直线l的方程,当l与x轴垂直时,通过计算,不满足题意,再设l:
在椭圆上,代入其标准方程,即可求出C的方程;(2)先设直线P2A与直线P2B的斜率分别为k1,k2,再设直线l的方程,当l与x轴垂直时,通过计算,不满足题意,再设l: ![]() (
(![]() ),将
),将![]() 代入
代入![]() ,写出判别式,利用根与系数的关系表示出x1+x2,x1x2,进而表示出
,写出判别式,利用根与系数的关系表示出x1+x2,x1x2,进而表示出![]() ,根据
,根据![]() 列出等式表示出
列出等式表示出![]() 和
和![]() 的关系,从而判断出直线恒过定点.
的关系,从而判断出直线恒过定点.
试题解析:(1)由于![]() ,
, ![]() 两点关于y轴对称,故由题设知C经过
两点关于y轴对称,故由题设知C经过![]() ,
, ![]() 两点.
两点.
又由![]() 知,C不经过点P1,所以点P2在C上.
知,C不经过点P1,所以点P2在C上.
因此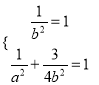 ,解得
,解得![]() .
.
故C的方程为![]() .
.
(2)设直线P2A与直线P2B的斜率分别为k1,k2,
如果l与x轴垂直,设l:x=t,由题设知![]() ,且
,且![]() ,可得A,B的坐标分别为(t,
,可得A,B的坐标分别为(t, ![]() ),(t,
),(t, ![]() ).
).
则![]() ,得
,得![]() ,不符合题设.
,不符合题设.
从而可设l: ![]() (
(![]() ).将
).将![]() 代入
代入![]() 得
得
![]()
由题设可知![]() .
.
设A(x1,y1),B(x2,y2),则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
而![]()
![]()
![]() .
.
由题设![]() ,故
,故![]() .
.
即![]() .
.
解得![]() .
.
当且仅当![]() 时,
时, ![]() ,欲使l:
,欲使l: ![]() ,即
,即![]() ,
,
所以l过定点(2, ![]() )
)
点睛:椭圆的对称性是椭圆的一个重要性质,判断点是否在椭圆上,可以通过这一方法进行判断;证明直线过定点的关键是设出直线方程,通过一定关系转化,找出两个参数之间的关系式,从而可以判断过定点情况.另外,在设直线方程之前,若题设中未告知,则一定要讨论直线斜率不存在和存在两种情况,其通法是联立方程,求判别式,利用根与系数的关系,再根据题设关系进行化简.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4—5:不等式选讲]
已知函数f(x)=–x2+ax+4,g(x)=│x+1│+│x–1│.
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[–1,1],求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取次序
1
2
3
4
5
6
7
8
零件尺寸
9.95
10.12
9.96
9.96
10.01
9.92
9.98
10.04
抽取次序
9
10
11
12
13
14
15
16
零件尺寸
10.26
9.91
10.13
10.02
9.22
10.04
10.05
9.95
经计算得
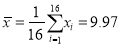 ,
, 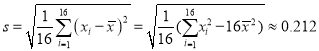 ,
, 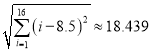 ,
, 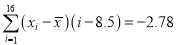 ,其中
,其中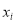 为抽取的第
为抽取的第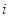 个零件的尺寸,
个零件的尺寸, 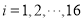 .
.(1)求
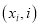
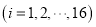 的相关系数
的相关系数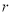 ,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若
,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若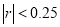 ,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).(2)一天内抽检零件中,如果出现了尺寸在
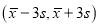 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.(ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查?
(ⅱ)在
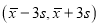 之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)附:样本
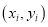
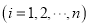 的相关系数
的相关系数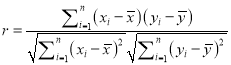 ,
, 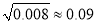 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b∈R,且ab≠0,则下列结论恒成立的是( )
A.a+b≥2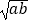
B.a2+b2>2ab
C. +
+ 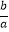 ≥2
≥2
D.| +
+ 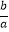 |≥2
|≥2 -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为
 (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为 .
.(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为
 ,求a.
,求a. -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4—5:不等式选讲]
已知函数f(x)=–x2+ax+4,g(x)=│x+1│+│x–1│.
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[–1,1],求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把函数f(x)=sin(2x+φ)(|φ|<
 )的图象上的所有点向左平移
)的图象上的所有点向左平移 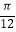 个单位长度,得到函数y=g(x)的图象,且g(﹣x)=g(x),则( )
个单位长度,得到函数y=g(x)的图象,且g(﹣x)=g(x),则( )
A.y=g(x)在(0, )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x=  对称
对称
B.y=g(x)在(0, )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x=  对称
对称
C.y=g(x)在(0, )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x=  对称
对称
D.y=g(x)在(0, )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x=  对称
对称
相关试题

