【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() ,
, ![]() 极坐标方程分别为
极坐标方程分别为![]() ,
, ![]() .
.
(Ⅰ)![]() 和
和![]() 交点的极坐标;
交点的极坐标;
(Ⅱ)直线![]() 的参数方程为
的参数方程为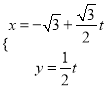 (
(![]() 为参数),
为参数),![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且与
,且与![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() .
.
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)联立![]() ,
, ![]() 极坐标方程,解出
极坐标方程,解出![]() ,反代得
,反代得![]() ,即得
,即得![]() 和
和![]() 交点的极坐标;(2)先利用
交点的极坐标;(2)先利用![]() 将
将![]() 极坐标方程化为直接坐标方程
极坐标方程化为直接坐标方程![]() ,再由直线参数方程几何意义得
,再由直线参数方程几何意义得![]() ,因此将直线
,因此将直线![]() 的参数方程代入
的参数方程代入![]() 直角坐标方程,利用韦达定理得
直角坐标方程,利用韦达定理得![]() ,且
,且![]() ,因此
,因此![]() .
.
试题解析:(Ⅰ)(方法一)由![]() ,
, ![]() 极坐标方程分别为
极坐标方程分别为![]() ,
, ![]() ’
’
化为平面直角坐标系方程分为![]() .
.
得交点坐标为![]() .
.
即![]() 和
和![]() 交点的极坐标分别为
交点的极坐标分别为![]() .
.
(方法二)解方程组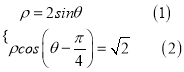
所以![]() ,
,
化解得![]() ,即
,即![]() ,
,
所以![]() 和
和![]() 交点的极坐标分别为
交点的极坐标分别为![]() .
.
(II)(方法一)化成普通方程解得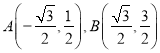
因为![]() ,所以
,所以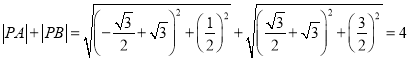 .
.
(方法二)把直线![]() 的参数方程:
的参数方程: 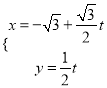 (
(![]() 为参数),代入
为参数),代入![]()
得![]() ,
, ![]() ,
,
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项数列
 为等比数列,等差数列
为等比数列,等差数列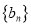 的前
的前 项和为
项和为 ,且满足:
,且满足: .
.(1)求数列
 ,
,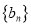 的通项公式;
的通项公式;(2)设
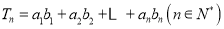 ,求
,求 ;
;(3)设
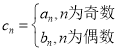 ,问是否存在正整数
,问是否存在正整数 ,使得
,使得 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体
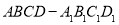 中,
中,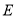 为棱
为棱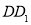 的中点.
的中点.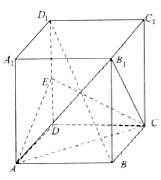
求证:(1)
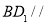 平面
平面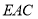 ;
;(2)平面
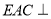 平面
平面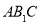 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
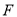 为抛物线
为抛物线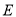 :
: 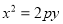 (
(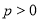 )的焦点,直线
)的焦点,直线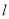 :
: 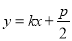 交抛物线
交抛物线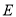 于
于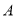 ,
, 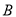 两点.
两点.(Ⅰ)当
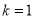 ,
, 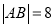 时,求抛物线
时,求抛物线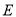 的方程;
的方程;(Ⅱ)过点
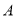 ,
, 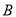 作抛物线
作抛物线 的切线,
的切线, 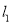 ,
, 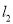 交点为
交点为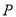 ,若直线
,若直线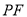 与直线
与直线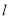 斜率之和为
斜率之和为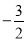 ,求直线
,求直线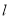 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
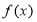 的单调区间;
的单调区间;(2)若
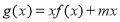 在区间
在区间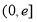 上的最大值为
上的最大值为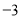 ,求
,求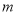 的值;
的值;(3)若
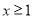 ,有不等式
,有不等式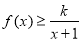 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
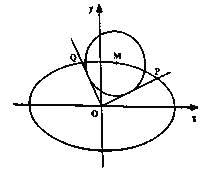
查看答案和解析>>【题目】如图,已知椭圆
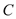 :
: 的离心率
的离心率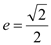 ,过点
,过点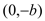 ,
,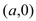 的直线与原点的距离为
的直线与原点的距离为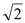 ,
,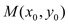 是椭圆上任一点,从原点
是椭圆上任一点,从原点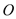 向圆
向圆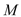 :
: 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点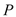 ,
,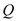 .
.
(Ⅰ)求椭圆
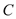 的方程;
的方程;(Ⅱ)若记直线
 ,
,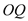 的斜率分别为
的斜率分别为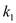 ,
,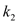 ,试求
,试求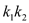 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
B. 在线性回归分析中,回归直线不一定过样本点的中心

C. 在回归分析中,
 为0.98的模型比
为0.98的模型比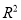 为0.80的模型拟合的效果好
为0.80的模型拟合的效果好D. 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
相关试题

