【题目】长为![]() 的线段
的线段![]() 的两个端点
的两个端点![]() 和
和![]() 分别在
分别在![]() 轴和
轴和![]() 轴上滑动.
轴上滑动.
(1)求线段![]() 的中点的轨迹
的中点的轨迹![]() 的方程;
的方程;
(2)当![]() 时,曲线
时,曲线![]() 与
与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 在线段
在线段![]() 上,过
上,过![]() 作
作![]() 轴的垂线交曲线
轴的垂线交曲线![]() 于不同的两点
于不同的两点![]() ,点
,点![]() 在线段
在线段![]() 上,满足
上,满足![]() 与
与![]() 的斜率之积为-2,试求
的斜率之积为-2,试求![]() 与
与![]() 的面积之比.
的面积之比.
参考答案:
【答案】(1)![]() (2)
(2)![]() .
.
【解析】试题分析:(1)设线段![]() 的中点为
的中点为![]() ,根据平面上两点间的距离公式,即可求解线段
,根据平面上两点间的距离公式,即可求解线段![]() 的中点的轨迹
的中点的轨迹![]() 的方程;
的方程;
(2)当![]() 时,直线
时,直线![]() 和直线
和直线![]() 的方程,联立方程组,求得点
的方程,联立方程组,求得点![]() 的坐标,即可得打结果.
的坐标,即可得打结果.
试题解析:
设线段![]() 的中点为
的中点为![]() ,则
,则![]() ,
, ![]() ,
,
故![]() ,
,
化简得![]() ,此即线段
,此即线段![]() 的中点的轨迹
的中点的轨迹![]() 的方程;
的方程;
【法二:当![]() 、
、![]() 重合或
重合或![]() 、
、![]() 重合时,
重合时, ![]() 中点到原点距离为
中点到原点距离为![]() ;
;
当![]() 、
、![]() 、
、![]() 不共线时,根据直角三角形斜边中线等于斜边的一半,知
不共线时,根据直角三角形斜边中线等于斜边的一半,知![]() 中点到原点距离也恒为
中点到原点距离也恒为![]() ,
,
故线段![]() 的中点的轨迹
的中点的轨迹![]() 的方程为
的方程为![]() 】
】
(2)当![]() 时,曲线
时,曲线![]() 的方程为
的方程为![]() ,它与
,它与![]() 轴的交点为
轴的交点为![]() 、
、![]() ,
,
设![]() ,
, ![]() ,
, ![]() ,
,
直线![]() 的斜率
的斜率![]() ,故直线
,故直线![]() 的斜率
的斜率![]() ,
,
直线![]() 的方程是
的方程是![]() ,
,
而直线![]() 的方程是
的方程是![]() ,即
,即![]()
联立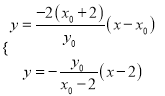 ,解得
,解得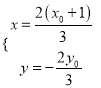 ,此即点
,此即点![]() 的坐标,
的坐标,
故 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,证明:
时,证明:  为偶函数;
为偶函数;(2)若
 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;(3)若
 ,求实数
,求实数 的取值范围,使
的取值范围,使 在
在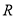 上恒成立.
上恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位从一所学校招收某类特殊人才,对20位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
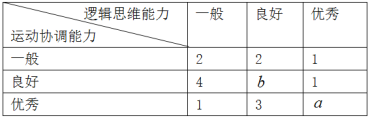
例如表中运动协调能力良好且逻辑思维能力一般的学生是4人,由于部分数据丢失,只知道从这20位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
 .
.(1)求
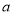 、
、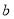 的值;
的值;(2)从运动协调能力为优秀的学生中任意抽取2位,求其中至少有一位逻辑思维能力优秀的学生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业实行裁员增效,已知现有员工
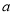 人,每人每年可创纯收益(已扣工资等)1万元,据评估,在生产条件不变的情况下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人每位0.4万元的生活费,并且企业正常运转所需人数不得少于现有员工的
人,每人每年可创纯收益(已扣工资等)1万元,据评估,在生产条件不变的情况下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人每位0.4万元的生活费,并且企业正常运转所需人数不得少于现有员工的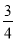 ,设该企业裁员
,设该企业裁员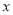 人后,年纯收益为
人后,年纯收益为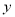 万元.
万元.(1)写出
 关于
关于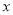 的函数关系式,并指出
的函数关系式,并指出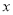 的取值范围;
的取值范围;(2)当
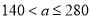 时,该企业应裁员多少人,才能获得最大的经济效益(注:在保证能取得最大的经济效益的情况下,能少裁员,应尽量少裁员)?
时,该企业应裁员多少人,才能获得最大的经济效益(注:在保证能取得最大的经济效益的情况下,能少裁员,应尽量少裁员)? -
科目: 来源: 题型:
查看答案和解析>>【题目】国家实行二孩生育政策后,为研究家庭经济状况对生二胎的影响,某机构在本地区符合二孩生育政策的家庭中,随机抽样进行了调查,得到如下的列联表:
经济状况好
经济状况一般
合计
愿意生二胎
50
不愿意生二胎
20
110
合计
210
(1)请完成上面的列联表,并判断能否在犯错误的概率不超过
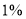 的前提下认为家庭经济状况与生育二胎有关?
的前提下认为家庭经济状况与生育二胎有关?(2)若采用分层抽样的方法从愿意生二胎的家庭中随机抽取4个家庭,则经济状况好和经济状况一般的家庭分别应抽取多少个?
(3)在(2)的条件下,从中随机抽取2个家庭,求2个家庭都是经济状况好的概率.
附:

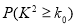
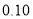
0.05
0.025
0.010
0.005
0.001
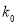
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 是定义在
是定义在 上的函数,并且满足下面三个条件:①对任意正数
上的函数,并且满足下面三个条件:①对任意正数 ,都有
,都有 ;②当
;②当 时,
时,  ;③
;③ .
.(1)求
 ,
,  的值;
的值;(2)证明
 在
在 上是减函数;
上是减函数;(3)如果不等式
 成立,求
成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
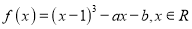 ,其中
,其中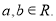
(Ⅰ)求
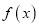 的单调区间;
的单调区间;(Ⅱ)若
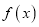 存在极值点
存在极值点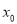 ,且
,且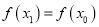 ,其中
,其中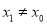 ,求证:
,求证: 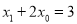 ;
;(Ⅲ)设
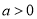 ,函数
,函数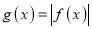 ,求证:
,求证: 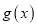 在区间
在区间 上最大值不小于
上最大值不小于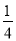 .
.
相关试题

