【题目】设函数![]() 是定义在
是定义在![]() 上的函数,并且满足下面三个条件:①对任意正数
上的函数,并且满足下面三个条件:①对任意正数![]() ,都有
,都有![]() ;②当
;②当![]() 时,
时, ![]() ;③
;③![]() .
.
(1)求![]() ,
, ![]() 的值;
的值;
(2)证明![]() 在
在![]() 上是减函数;
上是减函数;
(3)如果不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)见解析; (Ⅲ)
;(Ⅱ)见解析; (Ⅲ)![]() ).
).
【解析】试题分析:(1)利用赋值法,求![]() 、
、![]() 的值.
的值.
(2)利用单调性的定义,结合抽象函数之间的数值关系进行证明.
(3)利用函数的单调性将不等式进行转化,解不等式即可.
试题解析:
(Ⅰ)令![]() 易得
易得![]() .
.
而![]() ,
,
且![]() ,得
,得![]() .
.
(Ⅱ)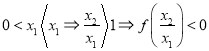
∴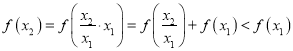
∴![]() 在
在![]() 上为减函数.
上为减函数.
(Ⅲ)由条件(1)及(Ⅰ)的结果得: ![]() ,其中
,其中![]() ,
,
由(Ⅱ)得: 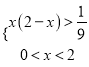 ,解得
,解得![]() 的范围是
的范围是![]() )
)
点晴:本题属于对函数单调性的证明和单调性应用的考察,若函数![]() 在区间上单调递增,则
在区间上单调递增,则![]() 时,有
时,有![]() ,事实上,若
,事实上,若![]() ,则
,则![]() ,这与
,这与![]() 矛盾,类似地,若
矛盾,类似地,若![]() 在区间上单调递减,则当
在区间上单调递减,则当![]() 时有
时有![]() ;据此可以解不等式,由函数值的大小,根据单调性就可以得自变量的大小关系.
;据此可以解不等式,由函数值的大小,根据单调性就可以得自变量的大小关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业实行裁员增效,已知现有员工
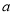 人,每人每年可创纯收益(已扣工资等)1万元,据评估,在生产条件不变的情况下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人每位0.4万元的生活费,并且企业正常运转所需人数不得少于现有员工的
人,每人每年可创纯收益(已扣工资等)1万元,据评估,在生产条件不变的情况下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人每位0.4万元的生活费,并且企业正常运转所需人数不得少于现有员工的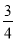 ,设该企业裁员
,设该企业裁员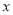 人后,年纯收益为
人后,年纯收益为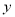 万元.
万元.(1)写出
 关于
关于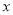 的函数关系式,并指出
的函数关系式,并指出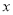 的取值范围;
的取值范围;(2)当
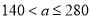 时,该企业应裁员多少人,才能获得最大的经济效益(注:在保证能取得最大的经济效益的情况下,能少裁员,应尽量少裁员)?
时,该企业应裁员多少人,才能获得最大的经济效益(注:在保证能取得最大的经济效益的情况下,能少裁员,应尽量少裁员)? -
科目: 来源: 题型:
查看答案和解析>>【题目】长为
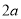 的线段
的线段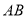 的两个端点
的两个端点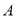 和
和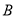 分别在
分别在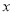 轴和
轴和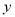 轴上滑动.
轴上滑动.(1)求线段
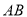 的中点的轨迹
的中点的轨迹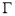 的方程;
的方程;(2)当
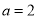 时,曲线
时,曲线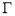 与
与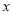 轴交于
轴交于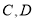 两点,点
两点,点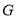 在线段
在线段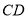 上,过
上,过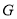 作
作 轴的垂线交曲线
轴的垂线交曲线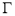 于不同的两点
于不同的两点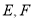 ,点
,点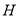 在线段
在线段 上,满足
上,满足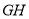 与
与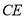 的斜率之积为-2,试求
的斜率之积为-2,试求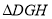 与
与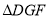 的面积之比.
的面积之比. -
科目: 来源: 题型:
查看答案和解析>>【题目】国家实行二孩生育政策后,为研究家庭经济状况对生二胎的影响,某机构在本地区符合二孩生育政策的家庭中,随机抽样进行了调查,得到如下的列联表:
经济状况好
经济状况一般
合计
愿意生二胎
50
不愿意生二胎
20
110
合计
210
(1)请完成上面的列联表,并判断能否在犯错误的概率不超过
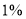 的前提下认为家庭经济状况与生育二胎有关?
的前提下认为家庭经济状况与生育二胎有关?(2)若采用分层抽样的方法从愿意生二胎的家庭中随机抽取4个家庭,则经济状况好和经济状况一般的家庭分别应抽取多少个?
(3)在(2)的条件下,从中随机抽取2个家庭,求2个家庭都是经济状况好的概率.
附:

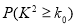
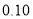
0.05
0.025
0.010
0.005
0.001
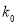
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
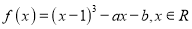 ,其中
,其中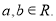
(Ⅰ)求
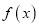 的单调区间;
的单调区间;(Ⅱ)若
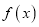 存在极值点
存在极值点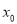 ,且
,且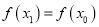 ,其中
,其中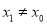 ,求证:
,求证: 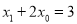 ;
;(Ⅲ)设
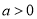 ,函数
,函数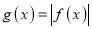 ,求证:
,求证: 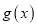 在区间
在区间 上最大值不小于
上最大值不小于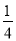 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分15分)已知椭圆
 :
: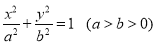 过点
过点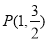 ,离心率为
,离心率为 .
.(Ⅰ)求椭圆
 的标准方程;
的标准方程;(Ⅱ)设
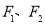 分别为椭圆
分别为椭圆 的左、右焦点,过
的左、右焦点,过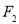 的直线
的直线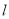 与椭圆
与椭圆 交于不同两点
交于不同两点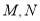 ,记
,记 的内切圆的面积为
的内切圆的面积为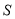 ,求当
,求当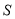 取最大值时直线
取最大值时直线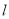 的方程,并求出最大值.
的方程,并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】交强险是车主必须为机动车购买的险种,若普通
 座以下私家车投保交强险第一年的费用(基准保费)统一为
座以下私家车投保交强险第一年的费用(基准保费)统一为 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
某机构为了研究某一品牌普通
 座以下私家车的投保情况,随机抽取了
座以下私家车的投保情况,随机抽取了 辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:类型






数量
10
5
5
20
15
5
以这
 辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:(Ⅰ)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定,
 ,记
,记 为某同学家里的一辆该品牌车在第四年续保时的费用,求
为某同学家里的一辆该品牌车在第四年续保时的费用,求 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损
 元,一辆非事故车盈利
元,一辆非事故车盈利 元:
元:①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至少有一辆事故车的概率;
②若该销售商一次购进
 辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
相关试题

