【题目】如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处. 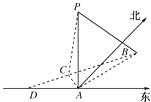
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
参考答案:
【答案】
(1)解:在Rt△PAB中,∠APB=60°,PA=1,∴AB= ![]() .
.
在Rt△PAC中,∠APC=30°,
∴AC= ![]() .
.
在△ACB中,∠CAB=30°+60°=90°,
∴BC= ![]() =
= ![]() =
= ![]() .
.
则船的航行速度为 ![]() ÷
÷ ![]() =2
=2 ![]() (千米/时)
(千米/时)
(2)解:在△ACD、中,∠DAC=90°﹣60°=30°,
sin∠DCA=sin(180°﹣∠ACB)=sin∠ACB= ![]() =
= ![]() =
= ![]()
![]() ,
,
sin∠CDA=sin(∠ACB﹣30°)
=sin∠ACBcos30°﹣cos∠ACBsin30°
= ![]()
![]()
![]() ﹣
﹣ ![]()
= ![]() .
.
由正弦定理得 ![]() =
= ![]() .
.
∴AD= ![]() =
= 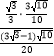 =
= ![]() .
.
故此时船距岛A有 ![]() 千米
千米
【解析】(1)先Rt△PAB、Rt△PAC中确定AB、AC的长,进而求得,∠CAB=30°+60°=90°,最后利用勾股定理求得BC,用里程除以时间即为船的速度.(2)利用sin∠DCA=sin(180°﹣∠ACB)=sin∠ACB求得sin∠DCA的值,利用sin∠CDA=sin(∠ACB﹣30°)=sin∠ACBcos30°﹣cos∠ACBsin30°求得sin∠CDA的值,进而利用正弦定理求得AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 上的点到两个焦点的距离之和为
上的点到两个焦点的距离之和为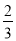 ,短轴长为
,短轴长为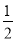 ,直线
,直线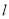 与椭圆
与椭圆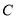 交于
交于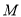 、
、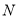 两点.
两点.(1)求椭圆
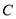 的方程;
的方程; (2)若直线
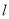 与圆
与圆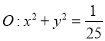 相切,探究
相切,探究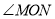 是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由.
是否为定值,如果是定值,请求出该定值;如果不是定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题
 “存在
“存在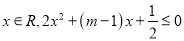 ”,命题
”,命题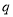 :“曲线
:“曲线 表示焦点在
表示焦点在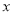 轴上的椭圆”,命题
轴上的椭圆”,命题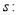 “曲线
“曲线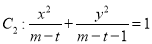 表示双曲线”
表示双曲线”(1)若“
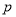 且
且 ”是真命题,求实数
”是真命题,求实数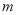 的取值范围;
的取值范围;(2)若
 是
是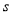 的必要不充分条件,求实数
的必要不充分条件,求实数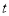 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方体
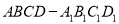 的棱长为
的棱长为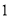 ,
, 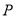 为
为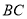 的中点,
的中点, 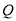 为线段
为线段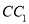 的动点,过
的动点,过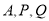 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为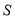 ,则下列命题正确的序号是_________.
,则下列命题正确的序号是_________.①当
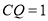 时,
时, 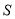 的面积为
的面积为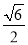 ;
; ②当
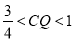 时,
时, 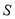 为六边形;
为六边形;③当
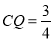 时,
时, 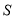 与
与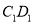 的交点
的交点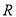 满足
满足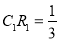 ;
; ④当
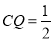 时,
时, 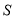 为等腰梯形;
为等腰梯形;⑤当
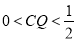 时,
时, 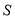 为四边形.
为四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,左顶点为
轴上,左顶点为 ,左焦点为
,左焦点为 ,点
,点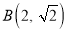 在椭圆
在椭圆 上,直线
上,直线 与椭圆
与椭圆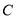 交于
交于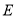 ,
,  两点,直线
两点,直线 ,
, 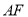 分别与
分别与 轴交于点
轴交于点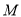 ,
, 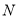 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)以
 为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
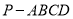 中,
中,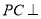 底面
底面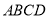 ,底面
,底面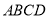 是直角梯形,
是直角梯形,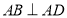 ,
,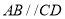 ,
,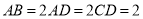 ,
,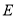 是
是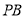 上的点.
上的点.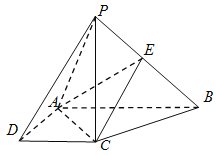
(Ⅰ)求证:平面
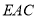 ⊥平面
⊥平面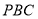 ;
; (Ⅱ)若
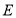 是
是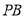 的中点,且二面角
的中点,且二面角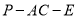 的余弦值为
的余弦值为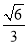 ,求直线
,求直线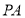 与平面
与平面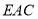 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的空间几何体
 中,四边形
中,四边形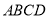 是边长为2的正方形,
是边长为2的正方形, 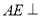 平面
平面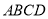 ,
, 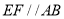 ,
, 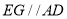 ,
,  ,
, 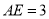 .
.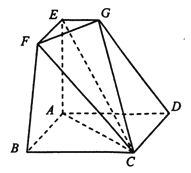
(1)求证:平面
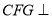 平面
平面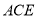 ;
;(2)求平面
 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
相关试题

