【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,左顶点为
轴上,左顶点为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)以![]() 为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)经过两定点
;(Ⅱ)经过两定点![]() ,
, ![]() .
.
【解析】试题分析:(Ⅰ)椭圆的左焦点为![]() ,所以
,所以![]() .由点
.由点![]() 在椭圆
在椭圆![]() 上,得
上,得![]() ,进而解出
,进而解出![]() 得到椭圆
得到椭圆![]() 的方程;(Ⅱ)直线
的方程;(Ⅱ)直线![]() 与椭圆
与椭圆![]() 联立,解得
联立,解得![]() 的坐标(用
的坐标(用![]() 表示),设出
表示),设出![]() ,
, ![]() 的方程,解出
的方程,解出![]() 的坐标,圆方程用
的坐标,圆方程用![]() 表示,最后可求得
表示,最后可求得![]() 为直径的圆经过两定点.
为直径的圆经过两定点.
试题解析:(Ⅰ) 设椭圆![]() 的方程为
的方程为![]() ,
,
因为椭圆的左焦点为![]() ,所以
,所以![]() .
.
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() .
.
由①②解得, ![]() ,
, ![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)因为椭圆![]() 的左顶点为
的左顶点为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .
.
因为直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
, ![]() ,
,
设点![]() (不妨设
(不妨设![]() ),则点
),则点![]() .
.
联立方程组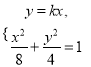 消去
消去![]() 得
得![]() .
.
所以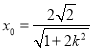 ,则
,则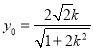 .
.
所以直线![]() 的方程为
的方程为![]() .
.
因为直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() ,
,
令![]() 得
得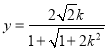 ,即点
,即点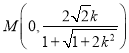 .
.
同理可得点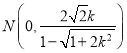 .
.
所以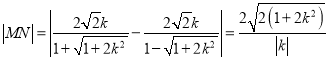 .
.
设![]() 的中点为
的中点为![]() ,则点
,则点![]() 的坐标为
的坐标为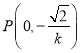 .
.
则以![]() 为直径的圆的方程为
为直径的圆的方程为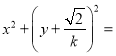
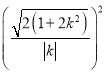 ,
,
即![]() .
.
令![]() ,得
,得![]() ,即
,即![]() 或
或![]() .
.
故以![]() 为直径的圆经过两定点
为直径的圆经过两定点![]() ,
, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题
 “存在
“存在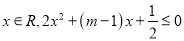 ”,命题
”,命题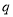 :“曲线
:“曲线 表示焦点在
表示焦点在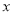 轴上的椭圆”,命题
轴上的椭圆”,命题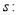 “曲线
“曲线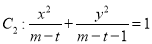 表示双曲线”
表示双曲线”(1)若“
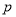 且
且 ”是真命题,求实数
”是真命题,求实数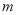 的取值范围;
的取值范围;(2)若
 是
是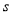 的必要不充分条件,求实数
的必要不充分条件,求实数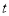 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方体
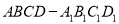 的棱长为
的棱长为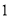 ,
, 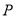 为
为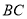 的中点,
的中点, 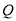 为线段
为线段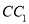 的动点,过
的动点,过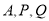 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为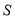 ,则下列命题正确的序号是_________.
,则下列命题正确的序号是_________.①当
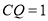 时,
时, 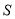 的面积为
的面积为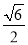 ;
; ②当
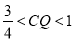 时,
时, 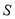 为六边形;
为六边形;③当
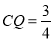 时,
时, 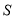 与
与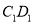 的交点
的交点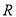 满足
满足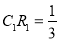 ;
; ④当
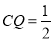 时,
时, 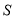 为等腰梯形;
为等腰梯形;⑤当
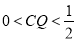 时,
时,  为四边形.
为四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
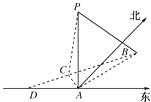
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
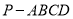 中,
中,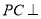 底面
底面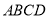 ,底面
,底面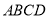 是直角梯形,
是直角梯形,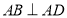 ,
,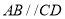 ,
,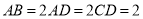 ,
,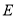 是
是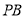 上的点.
上的点.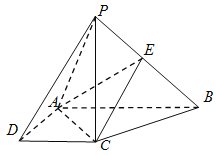
(Ⅰ)求证:平面
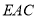 ⊥平面
⊥平面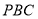 ;
; (Ⅱ)若
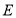 是
是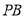 的中点,且二面角
的中点,且二面角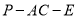 的余弦值为
的余弦值为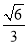 ,求直线
,求直线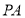 与平面
与平面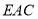 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
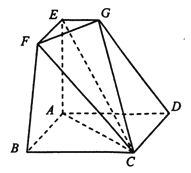
查看答案和解析>>【题目】如图所示的空间几何体
 中,四边形
中,四边形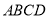 是边长为2的正方形,
是边长为2的正方形, 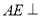 平面
平面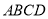 ,
, 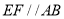 ,
, 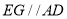 ,
,  ,
, 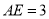 .
.
(1)求证:平面
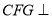 平面
平面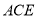 ;
;(2)求平面
 与平面
与平面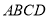 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】现如今,“网购”一词不再新鲜,越来越多的人已经接受并喜欢了这种购物方式,但随之也出现了商品质量不能保证与信誉不好等问题,因此,相关管理部门制定了针对商品质量与服务的评价体系,现从评价系统中选出成功交易200例,并对其评价进行统计:对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)依据题中的数据完成下表,并通过计算说明,能否有99.9%的把握认为“商品好评与服务好评”有关;
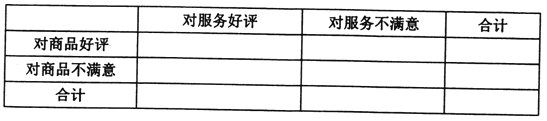
(2)若将频率视为概率,某人在该购物平台上进行了5次购物,设对商品和服务全好评的次数为随机变量
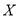 ,求
,求 的分布列(概率用算式表示)、数学期望和方差.
的分布列(概率用算式表示)、数学期望和方差.
相关试题

