【题目】已知两点![]() 及
及![]() ,点
,点![]() 在以
在以![]() 、
、![]() 为焦点的椭圆
为焦点的椭圆![]() 上,且
上,且![]() 、
、![]() 、
、![]() 构成等差数列.
构成等差数列.
(Ⅰ)求椭圆C的方程;
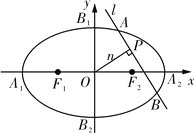
(Ⅱ)设![]() 是过原点的直线,
是过原点的直线,![]() 是与n垂直相交于
是与n垂直相交于![]() 点,与椭圆相交于
点,与椭圆相交于![]() 两点的直线,
两点的直线,![]() ,是否存在上述直线
,是否存在上述直线![]() 使
使![]() 成立?若存在,求出直线
成立?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(Ⅰ)由![]() 构成等差数列可得,
构成等差数列可得, ![]() ,
,![]() .又
.又![]() ,
,![]() ,从而可得结果;(Ⅱ)先证明当
,从而可得结果;(Ⅱ)先证明当![]() 与
与![]() 轴垂直时,不合题意,当
轴垂直时,不合题意,当![]() 与x轴不垂直时,设
与x轴不垂直时,设![]() 的方程为
的方程为![]() ,由
,由![]() 与
与![]() 垂直相交于
垂直相交于![]() 点且
点且![]() ,得
,得![]() ,利用韦达定理以及平面向量数量积公式,可得
,利用韦达定理以及平面向量数量积公式,可得![]() ,矛盾,故此时的直线
,矛盾,故此时的直线![]() 也不存在.
也不存在.
.试题解析:(Ⅰ)依题意,设椭圆![]() 的方程为
的方程为![]() .
.
![]()
![]() 构成等差数列,
构成等差数列,
![]()
![]() ,
,![]() .
.
又![]() ,
,![]() .
.
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,
,
假设存在直线![]() 使
使![]() 成立,
成立,
(ⅰ)当![]() 与
与![]() 轴垂直时,满足
轴垂直时,满足![]() 的直线
的直线![]() 的方程为
的方程为![]() 或
或![]()
当![]() 时,
时,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() .
.
∴![]()
当![]() 时,同理可得
时,同理可得![]() ,
,
即此时的直线![]() 不存在.
不存在.
(ⅱ)当![]() 与
与![]() 轴不垂直时,设
轴不垂直时,设![]() 的方程为
的方程为![]() ,
,
由![]() 与
与![]() 垂直相交于
垂直相交于![]() 点且
点且![]() ,得
,得![]() .
.
因为![]() ,
,![]() ,
,
![]() ,
,![]() .
.
将![]() 代入椭圆方程,得
代入椭圆方程,得![]()
由根与系数的关系得:![]()
![]() ,
,
![]()
即![]() ,矛盾,故此时的直线
,矛盾,故此时的直线![]() 也不存在.
也不存在.
综上可知,使![]() 成立的直线
成立的直线![]() 不存在.
不存在.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现采用随机模拟的方法估计一位射箭运动员三次射箭恰有两次命中的概率:先由计算机随机产生0到9之间取整数的随机数,指定1,2,3,4,5表示命中,6,7,8,9,0表示不命中,再以三个随机数为一组,代表三次射箭的结果,经随机模拟产生了如下20组随机数:
807 966 191 925 271 932 812 458 569 683
489 257 394 027 552 488 730 113 537 741
根据以上数据,估计该运动员三次射箭恰好有两次命中的概率为
A. 0.20 B. 0.25 C. 0.30 D. 0.50
-
科目: 来源: 题型:
查看答案和解析>>【题目】北京大学从参加逐梦计划自主招生考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组
 ,
, 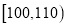 ,…,
,…, 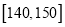 后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:(1)求分数在
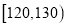 内的频率;
内的频率;(2)估计本次考试成绩的中位数(结果四舍五入,保留整数);
(3)用分层抽样的方法在分数段为
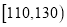 的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有
的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有 人在分数段
人在分数段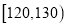 内的概率.
内的概率.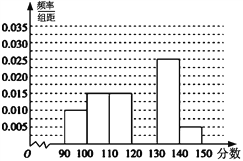
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱
 中,
中,  、
、 分别是
分别是 ,
,  的中点,已知
的中点,已知 与平面
与平面 所成的角为
所成的角为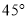 ,
,  .
.(1)证明:
 ∥平面
∥平面 ;
;(2)求二面角
 的正弦值.
的正弦值.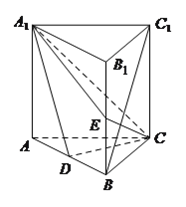
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 、
、 为常数).若函数
为常数).若函数 与
与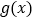 的图象在
的图象在 处相切,
处相切,(Ⅰ)求
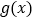 的解析式;
的解析式;(Ⅱ)设函数

 ,若
,若 在
在 上的最小值为
上的最小值为 ,求实数
,求实数 的值;
的值;(Ⅲ)设函数
 ,若
,若 在
在 上恒成立,求实数
上恒成立,求实数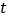 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过抛物线y2=2px(p>0)的焦点F的直线交抛物线于点A,B,交其准线l于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )
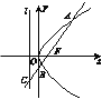
A. y2=9x B. y2=6x C. y2=3x D. y2=
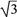 x
x -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线y=x+ln x在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a=________
相关试题

