【题目】解关于x的方程:
(1)lgx+lg(x﹣3)=1;
(2)![]() .
.
参考答案:
【答案】
(1)解:∵lgx+lg(x﹣3)=lg[x(x﹣3)]=lg(x2﹣3x)=1=lg10
∴x2﹣3x=10,∴x=﹣2或5
∵x>0,∴x=5
(2)解: ![]()
∴ ![]() ,∴x=3
,∴x=3
【解析】(1)将不等式转化为对数的真数的运算,转化为整式不等式解之;(2)利用指数的幂的运算解答.
【考点精析】根据题目的已知条件,利用函数的零点与方程根的关系的相关知识可以得到问题的答案,需要掌握二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
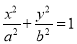 (a>b>0)的离心率为
(a>b>0)的离心率为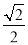 ,直线y=x+2过椭圆C的左焦点F1.
,直线y=x+2过椭圆C的左焦点F1.(1)求椭圆C的标准方程;
(2)设过点A(0,﹣1)的直线l与椭圆交于不同两点M、N,当△MON的面积为
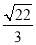 时,求直线l的方程.
时,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的钢板的边界
 是抛物线的一部分,且
是抛物线的一部分,且 垂直于抛物线对称轴,现欲从钢板上截取一块以
垂直于抛物线对称轴,现欲从钢板上截取一块以 为下底边的等腰梯形钢板
为下底边的等腰梯形钢板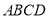 ,其中
,其中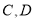 均在抛物线弧上.设
均在抛物线弧上.设 (米),且
(米),且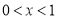 .
.(1)当
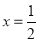 时,求等腰梯形钢板的面积;
时,求等腰梯形钢板的面积;(2)当
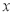 为何值时,等腰梯形钢板的面积最大?并求出最大值.
为何值时,等腰梯形钢板的面积最大?并求出最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+
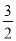 x2+mx在x=1处有极小值,
x2+mx在x=1处有极小值,g(x)=f(x)﹣
 x3﹣
x3﹣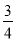 x2+x﹣alnx.
x2+x﹣alnx.(1)求函数f(x)的单调区间;
(2)是否存在实数a,对任意的x1、x2∈(0,+∞),且x1≠x2,有
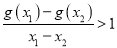 恒成立?若存在,求出a的取值范围;若不存在,说明理由.
恒成立?若存在,求出a的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρsin(θ+
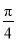 )=
)=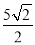 ,曲线C的参数方程为
,曲线C的参数方程为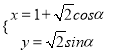 (α为参数).
(α为参数).(1)求直线l的普通方程;
(2)若P是曲线C上的动点,求点P到直线l的最大距离及点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
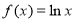 ,
,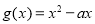 .
.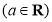
(Ⅰ)求
 的单调区间;
的单调区间;(Ⅱ)若
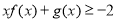 恒成立,求参数
恒成立,求参数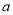 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
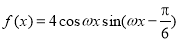 (
(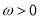 )的对称中心到对称轴距离的最小值为
)的对称中心到对称轴距离的最小值为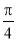 .
.(Ⅰ)求
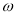 ;
;(Ⅱ)
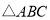 中,角
中,角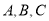 的对边分别为
的对边分别为 .已知锐角
.已知锐角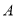 为函数
为函数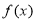 的一个零点,且
的一个零点,且 ,
,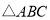 的面积
的面积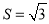 ,求
,求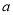 .
.
相关试题

