【题目】为迎接![]() 年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了
年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了![]() 名学生,将他们的比赛成绩(满分为
名学生,将他们的比赛成绩(满分为![]() 分)分为
分)分为![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于![]() 分”,估计
分”,估计![]() 的概率;
的概率;
(Ⅲ)在抽取的![]() 名学生中,规定:比赛成绩不低于
名学生中,规定:比赛成绩不低于![]() 分为“优秀”,比赛成绩低于
分为“优秀”,比赛成绩低于![]() 分为“非优秀”.请将下面的
分为“非优秀”.请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
参考公式及数据:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)见解析
(Ⅲ)见解析
【解析】
(Ⅰ)利用频率分布直方图小长方形的面积之和是1可得;
(Ⅱ)由题意利用频率近似概率可得;
(Ⅲ)由题意填写列联表,计算观测值,对照临界值得出结论.
(Ⅰ)由题可得![]() ,
,
解得![]() .
.
(Ⅱ)由(Ⅰ)知![]() ,
,
则比赛成绩不低于![]() 分的频率为
分的频率为![]() ,
,
故从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于![]() 分的概率约为
分的概率约为![]() .
.
(Ⅲ)由(Ⅱ)知,在抽取的![]() 名学生中,比赛成绩优秀的有
名学生中,比赛成绩优秀的有![]() 人,
人,
由此可得完整的![]() 列联表:
列联表:
优秀 | 非优秀 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
所以![]() 的观测值
的观测值![]() ,
,
所以没有![]() 的把握认为“比赛成绩是否优秀与性别有关”.
的把握认为“比赛成绩是否优秀与性别有关”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
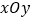 中,直线
中,直线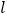 经过点
经过点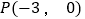 ,其倾斜角为
,其倾斜角为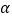 ,以原点
,以原点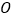 为极点,以
为极点,以 轴为非负半轴为极轴,与坐标系
轴为非负半轴为极轴,与坐标系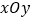 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线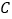 的极坐标方程为
的极坐标方程为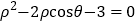 .
.(1)若直线
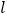 与曲线
与曲线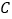 有公共点,求倾斜角
有公共点,求倾斜角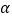 的取值范围;
的取值范围;(2)设
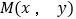 为曲线
为曲线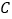 上任意一点,求
上任意一点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面使用类比推理,得到的结论正确的是( )
A. 直线
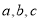 ,若
,若 ,则
,则 .类比推出:向量
.类比推出:向量 ,
, ,
, ,若
,若 ∥
∥ ,
, ∥
∥ ,则
,则 ∥
∥ .
.B. 三角形的面积为
 ,其中
,其中 ,
, ,
, 为三角形的边长,
为三角形的边长, 为三角形内切圆的半径,类比推出,可得出四面体的体积为
为三角形内切圆的半径,类比推出,可得出四面体的体积为 ,(
,( ,
, ,
, ,
, 分别为四面体的四个面的面积,
分别为四面体的四个面的面积, 为四面体内切球的半径)
为四面体内切球的半径)C. 同一平面内,直线
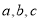 ,若
,若 ,则
,则 .类比推出:空间中,直线
.类比推出:空间中,直线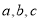 ,若
,若 ,则
,则 .
.D. 实数
 ,若方程
,若方程 有实数根,则
有实数根,则 .类比推出:复数
.类比推出:复数 ,若方程
,若方程 有实数根,则
有实数根,则 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, ,其中
,其中 ,(
,( ).
).(1)若函数
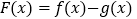 有极值
有极值 ,求
,求 的值;
的值;(2)若函数
 在区间
在区间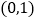 上为减函数,求
上为减函数,求 的取值范围;
的取值范围;(3)证明:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬中华传统文化,学校课外阅读兴趣小组进行每日一小时的“经典名著”和“古诗词”的阅读活动. 根据调查,小明同学阅读两类读物的阅读量统计如下:
小明阅读“经典名著”的阅读量
 (单位:字)与时间t(单位:分钟)满足二次函数关系,部分数据如下表所示;
(单位:字)与时间t(单位:分钟)满足二次函数关系,部分数据如下表所示;t
0
10
20
30

0
2700
5200
7500
阅读“古诗词”的阅读量
 (单位:字)与时间t(单位:分钟)满足如图1所示的关系.
(单位:字)与时间t(单位:分钟)满足如图1所示的关系.
(1)请分别写出函数
 和
和 的解析式;
的解析式;(2)在每天的一小时课外阅读活动中,小明如何分配“经典名著”和“古诗词”的阅读时间,使每天的阅读量最大,最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式
 ,对满足
,对满足 的一切实数
的一切实数 都成立,则实数
都成立,则实数 的取值范围为______
的取值范围为______ -
科目: 来源: 题型:
查看答案和解析>>【题目】某人在微信群中发了一个8元“拼手气”红包,被甲、乙、丙三人抢完,若三人均领到整数元,且每人至少领到1元,则甲领到的钱数不少于其他任何人的概率为
A.
 B.
B.  C.
C.  D.
D. 
相关试题

