【题目】已知全集U=R,集合A={x|x﹣2<0},B={x|﹣1<x<1},求:
(1)A∩B并说明集合A和集合B的关系,
(2)AB.
参考答案:
【答案】【解答】解:(1)由A中不等式解得:x<2,即A={x|x<2},
∵B={x|﹣1<x<1},
∴A∩B={x|﹣1<x<1}=B,
则BA;
(2)∵A={x|x<2},B={x|﹣1<x<1},
∴AB={x|x≤﹣1或1≤x<2}.
【解析】(1)求出A中不等式的解集确定出A,求出A与B的交集,判断出A与B的包含关系即可;
(2)根据全集A,求出B的补集即可.
【考点精析】关于本题考查的集合的交集运算和集合的补集运算,需要了解交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立;对于全集U的一个子集A,由全集U中所有不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作:CUA即:CUA={x|x∈U且x∈A};补集的概念必须要有全集的限制才能得出正确答案.
B,反之也成立;对于全集U的一个子集A,由全集U中所有不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作:CUA即:CUA={x|x∈U且x∈A};补集的概念必须要有全集的限制才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
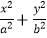 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 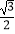 ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.
(1)求椭圆C的方程;
(2)已知直线l:y=kx+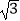 与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】命题p:关于x的方程x2+ax+2=0无实根,命题q:函数f(x)=logax在(0,+∞)上单调递增,若“p∧q”为假命题,“p∨q”真命题,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|1≤x≤7},B={x|﹣2m+1<x<m},全集为实数集R.
(1)若m=5,求A∪B,(RA)∩B;
(2)若A∩B=A,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
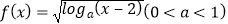 的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
(1)求(RA)∩B;
(2)若(A∪B)∩C≠,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某射击运动员每次射击击中目标的概率都为,现采用随机模拟的方法估计该运动员4次射击至少3次击中目标的概率:先由计算器产生0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,再以每4个随机数为一组,代表4次射击的结果,经随机模拟产生了如下20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
据此估计,该射击运动员4次射击至少3次击中目标的概率为__________.
相关试题

