【题目】自驾游从![]() 地到
地到![]() 地有甲乙两条线路,甲线路是
地有甲乙两条线路,甲线路是![]() ,乙线是
,乙线是![]() ,其中
,其中![]() 段、
段、![]() 段、
段、![]() 段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表1所示.经调查发现,堵车概率
段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表1所示.经调查发现,堵车概率![]() 在
在![]() 上变化,
上变化, ![]() 在
在![]() 上变化.在不堵车的情况下.走线路甲需汽油费500元,走线路乙需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计
上变化.在不堵车的情况下.走线路甲需汽油费500元,走线路乙需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计![]() 段平均堵车时间,调查了100名走甲线路的司机,得到表2数据.
段平均堵车时间,调查了100名走甲线路的司机,得到表2数据.
CD段 | EF段 | GH段 | |||
堵车概率 |
|
|
| ||
平均堵车时间 (单位:小时) |
| 2 | 1 | ||
(表1) | |||||
堵车时间(单位:小时) | 频数 | ||||
| 8 | ||||
| 6 | ||||
| 38 | ||||
| 24 | ||||
| 24 | ||||
(表2) | |||||
(1)求![]() 段平均堵车时间
段平均堵车时间![]() 的值.
的值.
(2)若只考虑所花汽油费期望值的大小,为了节约,求选择走甲线路的概率.
(3)在(2)的条件下,某4名司机中走甲线路的人数记为X,求X的数学期望。
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)用每一段的时间的平均值乘以对应的概率,即为所求;(2)先求出走线路甲所花汽油费的期望![]() ,再求出走乙线路多花汽油费的数学期望为
,再求出走乙线路多花汽油费的数学期望为![]() .择走甲线路应满足
.择走甲线路应满足![]() ,结合
,结合![]() 、
、![]() 的范围,利用几何概型求出选择走甲线路的概率;(3)根据二项分布的特征求其期望.
的范围,利用几何概型求出选择走甲线路的概率;(3)根据二项分布的特征求其期望.
试题解析:(1) ![]()
(2)设走线路甲所花汽油费为![]() 元,则
元,则![]()
法一:设走乙线路多花的汽油费为![]() 元,
元, ![]()
![]() 段、
段、![]() 段堵车与否相互独立,
段堵车与否相互独立,
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
![]() 走乙线路所花汽油费的数学期望为
走乙线路所花汽油费的数学期望为
![]()
依题意选择走甲线路应满足
![]() ,
,
![]()
![]()
![]()
(3)二项分布![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直角坐标平面内的两个点P和Q满足条件:①P和Q都在函数y=f(x)的图象上;②P和Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”([P,Q]与[Q,P]看作同一对“友好点对”).已知函数
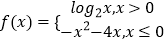 ,则此函数的“友好点对”有( )
,则此函数的“友好点对”有( )
A.0对
B.1对
C.2对
D.3对 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
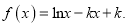
(Ⅰ)若
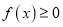 有唯一解,求实数
有唯一解,求实数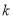 的值;
的值;(Ⅱ)证明:当
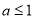 时,
时, 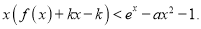
(附:
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据:
P(k2>k)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.83
x
2
4
5
6
8
y
30
40
60
50
70
(Ⅰ)画出散点图;
(Ⅱ)求回归直线方程;
(Ⅲ)试预测广告费支出为10万元时,销售额多大? -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 的定义域为 , 值域为 .
的定义域为 , 值域为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=ax(a>0,a≠1)在[﹣1,2]上的最大值为4,最小值为m,且函数g(x)=(1﹣4m)
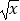 在[0,+∞)上是增函数,则m= , a= .
在[0,+∞)上是增函数,则m= , a= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如果定义在(﹣∞,0)∪(0,+∞)上的奇函数f(x)在(0,+∞)内是减函数,又有f(3)=0,则f(x)>0的解集为 , xf(x)<0的解集为 .
相关试题

