【题目】△ABC中,A(0,1),AB边上的高线方程为x+2y-4=0,AC边上的中线方程为2x+y-3=0,求AB,BC,AC边所在的直线方程
参考答案:
【答案】![]() ,
,![]() ,
,![]()
【解析】
试题分析:先找出AB边上的高线方程的斜率,根据两直线垂直时斜率乘积为-1求出直线AB的斜率和A的坐标,即可写出直线AB的方程;把直线AB与AC边上的中线方程联立求出交点B的坐标,然后设出AC的中点D和C的坐标,根据中点坐标公式列出方程组,求出解即可得到C的坐标,利用两点坐标写出直线BC的方程;由A和C的坐标写出直线AC的方程即可
试题解析:直线AB的斜率为2,∴AB边所在的直线方程为![]() ,
,
直线AB与AC边中线的方程交点为![]()
设AC边中点D(x1,3-2x1),C(4-2y1,y1),∵D为AC的中点,由中点坐标公式得
![]() 边所在的直线方程为
边所在的直线方程为![]() ;
;
AC边所在的直线方程为y=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
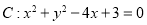 ,过原点的直线
,过原点的直线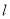 与其交于不同的两点
与其交于不同的两点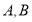 .
.(1)求直线
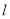 斜率
斜率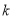 的取值范围;
的取值范围;(2)求线段
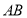 的中点
的中点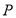 的轨迹
的轨迹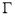 的方程;
的方程;(3)若直线
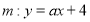 与曲线
与曲线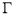 只有一个公共点,求
只有一个公共点,求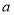 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=
 AP=2,D是AP的中点,E,F,G分别是PC,PD,CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图(2).
AP=2,D是AP的中点,E,F,G分别是PC,PD,CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图(2).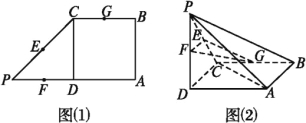
(1)求证:AP∥平面EFG;
(2)求三棱锥P-ABC的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明“自然数a,b,c中恰有一个偶数”时,下列假设正确的是 ( )
A.假设a,b,c都是奇数或至少有两个偶数
B.假设a,b,c都是偶数
C.假设a,b,c至少有两个偶数
D.假设a, b,c都是奇数
-
科目: 来源: 题型:
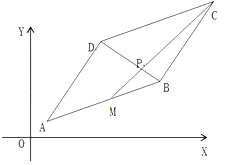
查看答案和解析>>【题目】在平行四边形
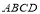 中,
中,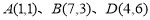 ,点
,点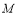 是线段
是线段 的中点线段
的中点线段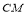 与
与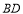 交于点
交于点 .
.
(1)求直线
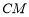 的方程;
的方程;(2)求点
 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
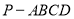 中,
中,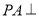 底面
底面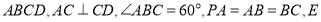 是
是 的中点.
的中点.(1)证明:
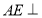 平面
平面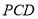 ;
;(2)求
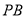 和平面
和平面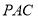 所成的角的正切值.
所成的角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.

(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
相关试题

