【题目】已知函数![]() ,
, ![]() 且
且![]() .
.
(Ⅰ)当![]() 时,令
时,令![]() ,
, ![]() 为常数,求函数
为常数,求函数![]() 的零点的个数;
的零点的个数;
(Ⅱ)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】试题分析:
(1)首先对函数求导,然后结合导函数与原函数的关系可得:
当![]() 时,函数
时,函数![]() 有一个零点;
有一个零点;
当![]() 时,函数
时,函数![]() 没有零点;
没有零点;
当![]() 时,函数
时,函数![]() 有两个零点.
有两个零点.
(2)首先求解![]() ,据此分类讨论求解函数的最小值,最后结合恒成立的条件可求得实数
,据此分类讨论求解函数的最小值,最后结合恒成立的条件可求得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)当![]() 时,
时, ![]() ,
, ![]()
所以![]()
令![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递减
上单调递减
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增
上单调递增
所以![]() 是
是![]() 的极小值点,
的极小值点, ![]() 的最小值为
的最小值为![]()
当![]() ,即
,即![]() 时,函数
时,函数![]() 有一个零点
有一个零点
当![]() ,即
,即![]() 时,函数
时,函数![]() 没有零点
没有零点
当![]() ,即
,即![]() 时,函数
时,函数![]() 有两个零点
有两个零点
(Ⅱ)由已知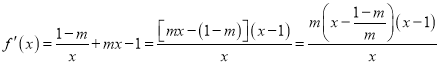
令![]() ,解得
,解得![]() .
.
由于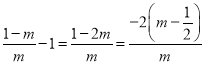
①若![]() ,则
,则![]() ,故当
,故当![]() 时,
时, ![]() ,因此
,因此![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,又因为
,又因为![]()
则![]() 不成立
不成立
②若![]() ,则
,则![]() ,故当
,故当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
所以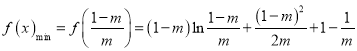
因为![]() ,所以
,所以![]()
则![]()
因此当![]() 时,
时, ![]() 恒成立
恒成立
③若![]() ,则
,则![]() ,故当
,故当![]() 时,
时, ![]() ,因此
,因此![]() 在
在![]() 上单调递增,
上单调递增,
故![]() ,令
,令![]() ,化简得
,化简得![]()
解得![]() ,所以
,所以![]()
综上所述,实数![]() 的取值范围是
的取值范围是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱柱
 中,侧面
中,侧面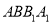 为矩形,
为矩形, 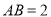 ,
, 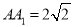 ,
, 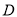 是
是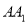 的中点,
的中点, 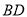 与
与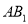 交于点
交于点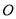 ,且
,且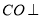 平面
平面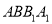 .
.(Ⅰ)证明:平面
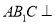 平面
平面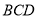 ;
;(Ⅱ)若
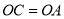 ,
, 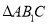 的重心为
的重心为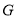 ,求直线
,求直线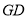 与平面
与平面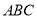 所成角的正弦值.
所成角的正弦值.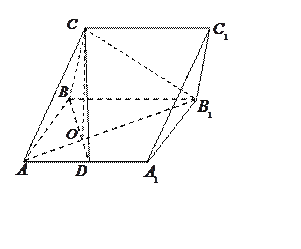
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科技公司生产一种手机加密芯片,其质量按测试指标划分为:指标大于或等于
 为合格品,小于
为合格品,小于 为次品.现随机抽取这种芯片共
为次品.现随机抽取这种芯片共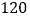 件进行检测,检测结果统计如表:
件进行检测,检测结果统计如表:测试指标

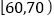

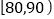
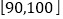
芯片数量(件)


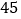
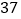

已知生产一件芯片,若是合格品可盈利
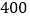 元,若是次品则亏损
元,若是次品则亏损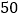 元.
元.(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产
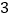 件芯片所获得的利润不少于
件芯片所获得的利润不少于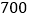 元的概率.
元的概率.(Ⅱ)记
 为生产
为生产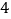 件芯片所得的总利润,求随机变量
件芯片所得的总利润,求随机变量 的分布列和数学期望
的分布列和数学期望 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲所示,
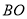 是梯形
是梯形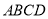 的高,
的高, 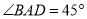 ,
, 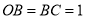 ,
, 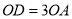 ,先将梯形
,先将梯形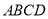 沿
沿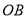 折起如图乙所示的四棱锥
折起如图乙所示的四棱锥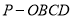 ,使得
,使得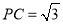 ,点
,点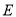 是线段
是线段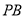 上一动点.
上一动点. 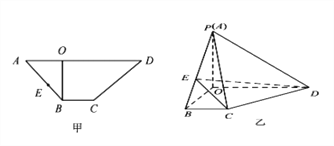
(1)证明:
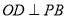 ;
;(2)当
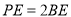 时,求
时,求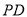 与平面
与平面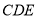 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个均匀的正方体玩具,各个面上分别写有1,2,3,4,5,6,将这个玩具先后抛掷2次,求:
(1)朝上的一面数相等的概率;
(2)朝上的一面数之和小于5的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】团购已成为时下商家和顾客均非常青睐的一种省钱、高校的消费方式,不少商家同时加入多家团购网.现恰有三个团购网站在
 市开展了团购业务,
市开展了团购业务,  市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.
市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.(1)从所调查的50家商家中任选两家,求他们加入团购网站的数量不相等的概率;
(2)从所调查的50家商家中任取两家,用
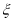 表示这两家商家参加的团购网站数量之差的绝对值,求随机变量
表示这两家商家参加的团购网站数量之差的绝对值,求随机变量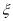 的分布列和数学期望;
的分布列和数学期望;(3)将频率视为概率,现从
 市随机抽取3家已加入团购网站的商家,记其中恰好加入了两个团购网站的商家数为
市随机抽取3家已加入团购网站的商家,记其中恰好加入了两个团购网站的商家数为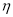 ,试求事件“
,试求事件“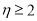 ”的概率.
”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=sinxcosx将 f(x)的图象向右平移
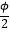 (0<φ<π) 个单位,得到y=g(x)图象且g(x)的一条对称轴是直线x=
(0<φ<π) 个单位,得到y=g(x)图象且g(x)的一条对称轴是直线x=  .
.
(1)求φ;
(2)求函数y=g(x)的单调增区间.
相关试题

