【题目】设点O为坐标原点,椭圆![]() 的右顶点为A,上顶点为B,过点O且斜率为
的右顶点为A,上顶点为B,过点O且斜率为![]() 的直线与直线AB相交M,且
的直线与直线AB相交M,且![]() .
.
(Ⅰ)求证:a=2b;
(Ⅱ)PQ是圆C:(x-2)2+(y-1)2=5的一条直径,若椭圆E经过P,Q两点,求椭圆E的方程.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:
(1)利用向量共线的充要条件计算可得a=2b;
(2)利用(1)中的结论联立直线与椭圆的方程,利用根与系数的关系计算可得椭圆E的方程是![]() .
.
试题解析:
(Ⅰ)∵A(a,0),B(0,b),![]() ,所以
,所以![]() ,
,
∴![]() ,解得a=2b,
,解得a=2b,
(Ⅱ)由(Ⅰ)知a=2b,∴椭圆E的方程为![]() 即x2+4y2=4b2(1)
即x2+4y2=4b2(1)
依题意,圆心C(2,1)是线段PQ的中点,且![]() .
.
由对称性可知,PQ与x轴不垂直,设其直线方程为y=k(x-2)+1,
代入(1)得:
(1+4k2)x2-8k(2k-1)x+4(2k-1)2-4b2=0
设P(x1,y1),Q(x2,y2),则![]() ,
,![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() .
.
从而x1x2=8-2b2.
于是![]()
解得b2=4,a2=16,∴椭圆E的方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民自来水收费标准如下:每户每月用水不超过5吨时,每吨为
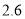 元,当用水超过5吨时,超过部分每吨4元。某月甲、乙两户共交水费
元,当用水超过5吨时,超过部分每吨4元。某月甲、乙两户共交水费 元,已知甲、乙两户该月用水量分别为
元,已知甲、乙两户该月用水量分别为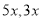 吨。
吨。(1)求
 关于
关于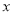 的函数。
的函数。(2)若甲、乙两户该月共交水费
 元,分别求甲、乙两户该月的用水量和水费。
元,分别求甲、乙两户该月的用水量和水费。 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 :
:  ,曲线
,曲线 :
:  (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,  轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.(Ⅰ)求曲线
 ,
,  的极坐标方程;
的极坐标方程;(Ⅱ)曲线
 :
:  (
( 为参数,
为参数,  ,
,  )分别交
)分别交 ,
,  于
于 ,
,  两点,当
两点,当 取何值时,
取何值时,  取得最大值.
取得最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表.已知从全部210人中随机抽取1人为优秀的概率为
 .
.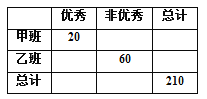
(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
(2)从全部210人中有放回地抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望E(ξ).
P(K2≥k0)
0.05
0.01
k0
3.841
6.635
附:
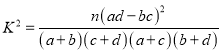
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,均值与方差都不变;
②设有一个回归方程
 ,变量x增加一个单位时,y平均增加3个单位;
,变量x增加一个单位时,y平均增加3个单位;③线性回归方程
 必经过点
必经过点 ;
;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说现有100人吸烟,那么其中有99人患肺病.其中错误的个数是( )
A. 0
B. 1
C. 2
D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班从6名班干部中(其中男生4人,女生2人),任选3人参加学校的义务劳动.
(1)设所选3人中女生人数为ξ,求ξ的分布列;
(2)求男生甲或女生乙被选中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知以点C为圆心的圆经过点A(-1,0)和B(3,4),且圆心在直线x+3y-15=0上.设点P在圆C上,求△PAB的面积的最大值.
相关试题

