【题目】设椭圆方程![]() +
+![]() =1(a>b>0),椭圆上一点到两焦点的距离和为4,过焦点且垂直于x轴的直线交椭圆于A,B两点,AB=2.
=1(a>b>0),椭圆上一点到两焦点的距离和为4,过焦点且垂直于x轴的直线交椭圆于A,B两点,AB=2.
(1)求椭圆方程;
(2)若M,N是椭圆C上的点,且直线OM与ON的斜率之积为﹣![]() ,是否存在动点P(x0,y0),若
,是否存在动点P(x0,y0),若![]() =
=![]() +2
+2![]() ,有x02+2y02为定值
,有x02+2y02为定值
参考答案:
【答案】(1)![]() (2)存在这样的点P(x0,y0)
(2)存在这样的点P(x0,y0)
【解析】
试题分析:(1)由已知得2a=4,![]() ,由此能求出椭圆方程;(2)存在这样的点P
,由此能求出椭圆方程;(2)存在这样的点P![]() .设M
.设M ![]() ,N
,N ![]() ,由
,由![]() ,结合已知条件能推导出存在这样的点P(x0,y0)
,结合已知条件能推导出存在这样的点P(x0,y0)
试题解析:(1)因为2a=4,所以,a=2,(2分)
∵过焦点且垂直于x轴的直线交椭圆于A,B两点,AB=2.
∴由椭圆的对称性知,椭圆过点(c,1),即![]() ,(4分)
,(4分)
c2=4﹣b2,解得b2=2,椭圆方程为![]() .(7分)
.(7分)
(2)存在这样的点P(x0,y0).设M(x1,y1),N(x2,y2),
则kOMkON=![]() =﹣
=﹣![]() ,化简为x1x2+2y1y2=0,(9分)
,化简为x1x2+2y1y2=0,(9分)
∵M,N是椭圆C上的点,∴![]() ,
,![]() ,
,
由![]() =
=![]() ,得
,得 ,(12分)
,(12分)
∵![]() =(x1+2x2)2+(y1+2y2)2
=(x1+2x2)2+(y1+2y2)2
=(![]() )+4(
)+4(![]() )+4(x1x2+2y1y2)=4+4×4+0=20,
)+4(x1x2+2y1y2)=4+4×4+0=20,
即存在这样的点P(x0,y0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在坐标原点
 的椭圆
的椭圆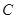 经过点
经过点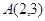 ,且点
,且点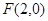 为其右焦点.
为其右焦点.(Ⅰ)求椭圆
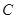 的标准方程;
的标准方程;(Ⅱ)是否存在平行于
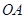 的直线
的直线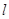 ,使得直线
,使得直线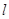 与椭圆
与椭圆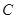 有公共点,且直线
有公共点,且直线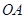 与
与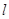 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线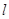 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某几何体的三视图如图所示,则它的外接球表面积为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
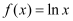 ,
,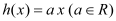 .
.(Ⅰ)函数
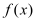 的图象与
的图象与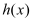 的图象无公共点,求实数
的图象无公共点,求实数 的取值范围;
的取值范围;(Ⅱ)是否存在实数
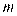 ,使得对任意的
,使得对任意的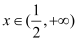 ,都有函数
,都有函数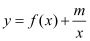 的图象在
的图象在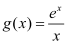 的图象的下方?若存在,请求出整数
的图象的下方?若存在,请求出整数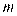 的最大值;若不存在,请说理由.
的最大值;若不存在,请说理由.(参考数据:
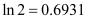 ,
,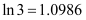 ,
,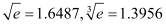 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知过点
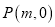 的直线
的直线 的参数方程是
的参数方程是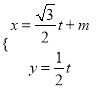 (
(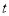 为参数).以平面直角坐标系的原点为极点,
为参数).以平面直角坐标系的原点为极点,  轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线 的极坐标方程式为
的极坐标方程式为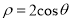 .
.(Ⅰ)求直线
 的普通方程和曲线
的普通方程和曲线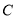 的直角坐标方程;
的直角坐标方程;(Ⅱ)若直线
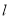 与曲线
与曲线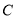 交于两点
交于两点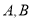 ,且
,且 ,求实数
,求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取
 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为 ,
, ,
, ,
, ,由此得到样本的重量频率分布直方图(如图).
,由此得到样本的重量频率分布直方图(如图).
(Ⅰ)求
 的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;(Ⅱ)从盒子中随机抽取
 个小球,其中重量在
个小球,其中重量在 内的小球个数为
内的小球个数为 ,求
,求 的分布列和数学期望. (以直方图中的频率作为概率).
的分布列和数学期望. (以直方图中的频率作为概率). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知国家某5A级大型景区对拥挤等级与每日游客数量
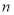 (单位:百人)的关系有如下规定:当
(单位:百人)的关系有如下规定:当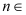
 时,拥挤等级为“优”;当
时,拥挤等级为“优”;当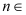
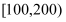 时,拥挤等级为“良”;当
时,拥挤等级为“良”;当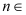
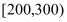 时,拥挤等级为“拥挤”;当
时,拥挤等级为“拥挤”;当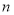
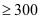 时,拥挤等级为“严重拥挤”。该景区对6月份的游客数量作出如图的统计数据:
时,拥挤等级为“严重拥挤”。该景区对6月份的游客数量作出如图的统计数据: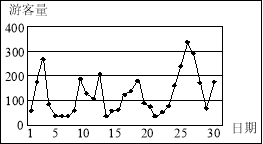
(Ⅰ)下面是根据统计数据得到的频率分布表,求出
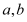 的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);游客数量
(单位:百人)

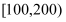
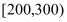
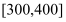
天数
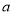

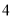
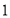
频率
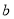
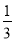
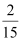
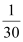
(Ⅱ)某人选择在6月1日至6月5日这5天中任选2天到该景区游玩,求他这2天遇到的游客拥挤等级均为“优”的概率.
相关试题

