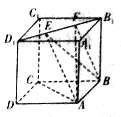
【题目】如图所示,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,则下列结论中正确结论的序号是__________.
,则下列结论中正确结论的序号是__________.
①![]() ;
;
②直线![]() 与平面
与平面![]() 所成角的正弦值为定值
所成角的正弦值为定值![]() ;
;
③当![]() 为定值,则三棱锥
为定值,则三棱锥![]() 的体积为定值;
的体积为定值;
④异面直线![]() 所成的角的余弦值为定值
所成的角的余弦值为定值![]() .
.
参考答案:
【答案】①③
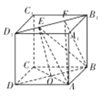
【解析】连接![]() ,交
,交![]() 于点
于点![]() .很明显
.很明显![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,①正确;
,①正确;
由AC⊥平面BB1D1D,得OE是AE在平面BB1D1D上的射影,所以∠AEO是直线AE与平面DBB1D1所成角,由于AE不是定值,所以②不正确;
由于点B到直线B1D1的距离不变,故△BEF的面积为定值,又点A到平面BEF的距离为![]() ,故三棱锥E-ABF的体积为定值,故③正确;
,故三棱锥E-ABF的体积为定值,故③正确;
当E在D1,F在B1,此时异面直线AE,BF所成的角为![]() ,故④不正确;
,故④不正确;
应填:①③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于数集
 ,其中
,其中 ,
,  ,定义向量集
,定义向量集 .若对于任意
.若对于任意 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .例如
.例如 具有性质
具有性质 .
.(
 )若
)若 ,且
,且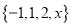 具有性质
具有性质 ,求
,求 的值.
的值.(
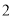 )若
)若 具有性质
具有性质 ,求证:
,求证:  ,且当
,且当 时,
时,  .
.(
 )若
)若 具有性质
具有性质 ,且
,且 ,
,  (
( 为常数),求有穷数列
为常数),求有穷数列 ,
,  ,
,  ,
,  的通项公式.
的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
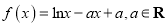 .
.(1)求函数
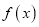 的单调区间;
的单调区间;(2)当
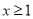 时,函数
时,函数 的图象恒不在
的图象恒不在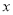 轴的上方,求实数
轴的上方,求实数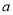 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
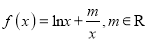
(Ⅰ)当
 (
( 为自然对数的底数)时,求
为自然对数的底数)时,求 的极小值;
的极小值;(Ⅱ)若函数
 存在唯一零点,求
存在唯一零点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年全国数学奥赛试行改革:在高二一年中举行5次全区竞赛,学生如果其中2次成绩达全区前20名即可进入省队培训,不用参加其余的竞赛,而每个学生最多也只能参加5次竞赛.规定:若前4次竞赛成绩都没有达全区前20名,则第5次不能参加竞赛.假设某学生每次成绩达全区前20名的概率都是
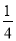 ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为
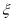 ,求
,求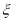 的分布列及
的分布列及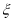 的数学期望.
的数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市拟兴建九座高架桥,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
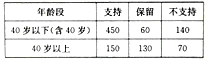
(1)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在40岁以下(含40岁)的人有多少被抽取;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在40岁以上的概率.
-
科目: 来源: 题型:
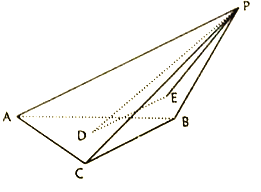
查看答案和解析>>【题目】如图,在三棱锥
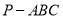 中,
中, 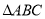 是正三角形,面
是正三角形,面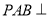 面
面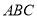 ,
, 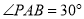 ,
, 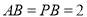 ,
, 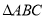 和
和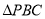 的重心分别为
的重心分别为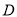 ,
,  .
.
(1)证明:
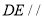 面
面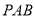 ;
;(2)求
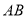 与面
与面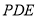 所成角的正弦值.
所成角的正弦值.
相关试题

