搜索
【题目】一袋中有大小相同的4个红球和2个白球，给出下列结论：
从中任取3球，恰有一个白球的概率是
；
从中有放回的取球6次，每次任取一球，则取到红球次数的方差为
；
从中有放回的取球3次，每次任取一球，则至少有一次取到红球的概率为
．
其中所有正确结论的序号是______ ．
参考答案：
【答案】
【解析】分析：①所求概率为
，计算即得结论；
②利用取到红球次数
可知其方差为
；
通过每次取到红球的概率
可知所求概率为
．
详解：①从中任取3球，恰有一个白球的概率是
，故正确；
②从中有放回的取球6次，每次任取一球，
取到红球次数，其方差为，故正确；
③从中有放回的取球3次，每次任取一球，每次取到红球的概率，
∴至少有一次取到红球的概率为，故正确．
故答案为：①②③．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某“双一流A类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查，其中一项是他们的月薪收入情况，调查发现，他们的月薪收入在人民币1.65万元到2.35万元之间，根据统计数据分组，得到如下的频率分布直方图：
（1）为感谢同学们对这项调查工作的支持，该校利用分层抽样的方法从样本的前两组中抽出6人，各赠送一份礼品，并从这6人中再抽取2人，各赠送某款智能手机1部，求获赠智能手机的2人月薪都不低于1.75万元的概率；
（2）同一组数据用该区间的中点值作代表.
（i）求这100人月薪收入的样本平均数
和样本方差
；（ii）该校在某地区就业的2018届本科毕业生共50人，决定于2019国庆长假期间举办一次同学联谊会，并收取一定的活动费用，有两种收费方案：
方案一：设
，月薪落在区间
左侧的每人收取400元，月薪落在区间内的每人收到600元，月薪落在区间右侧的每人收取800元.方案二：按每人一个月薪水的3%收取；用该校就业部统计的这100人月薪收入的样本频率进行估算，哪一种收费方案能收到更多的费用？
参考数据：
. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
．（1）若对于
，
恒成立，求实数
的取值范围；（2）若对于
，
恒成立，求实数的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知数列{xn}满足：x1=1，xn=xn+1+ln（1+xn+1）（n∈N*），证明：当n∈N*时，
（Ⅰ）0＜xn+1＜xn；
（Ⅱ）2xn+1﹣xn≤
；
（Ⅲ）
≤xn≤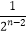 
． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知
，函数
，
.（1）若
在
上单调递增，求正数
的最大值；（2）若函数
在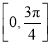
内恰有一个零点，求
的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】设{an}和{bn}是两个等差数列，记cn=max{b1﹣a1n，b2﹣a2n，…，bn﹣ann}（n=1，2，3，…），其中max{x1 ， x2 ， …，xs}表示x1 ， x2 ， …，xs这s个数中最大的数．（13分）
（1）若an=n，bn=2n﹣1，求c1 ， c2 ， c3的值，并证明{cn}是等差数列；
（2）证明：或者对任意正数M，存在正整数m，当n≥m时，
＞M；或者存在正整数m，使得cm ， cm+1 ， cm+2 ， …是等差数列． -
科目： 来源： 题型：
查看答案和解析>>【题目】中国古代数学名著《九章算术》中“竹九节”问题曰：“今有竹九节，下三节容量四升，上四节容量三升，问中间两节欲均容各多少？”其意为：“现有一根9节的竹子，自上而下的容积成等差数列，下面3节容量为4升，上面4节容积为3升，问中间2节各多少容积？”则中间2节容积合计________升
相关试题
