【题目】某种商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量,公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到![]() 元,公司拟投入
元,公司拟投入![]() 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入![]() 作为浮动宣传费用.试问:当该商品明年的销售量
作为浮动宣传费用.试问:当该商品明年的销售量![]() 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
参考答案:
【答案】(1)每件定价最多为![]() 元;(2)当该商品明年的销售量
元;(2)当该商品明年的销售量![]() 至少达到
至少达到![]() 万件时,才可能使明年的销售收入不低于原收入与总收入之和,此时该商品的每件定价为
万件时,才可能使明年的销售收入不低于原收入与总收入之和,此时该商品的每件定价为![]() 元.
元.
【解析】
试题分析:(1)设每件定价为![]() 元,依题意,得
元,依题意,得![]() ,解不等式即可求解结论;(2)依题意
,解不等式即可求解结论;(2)依题意![]() 时,不等式
时,不等式![]() 有解,等价于
有解,等价于![]() 时,得到
时,得到![]() 有解,利用基本不等式,即可得到结论.
有解,利用基本不等式,即可得到结论.
试题解析:(1)设每件定价为![]() 元,
元,
依题意,有![]() ,
,
整理得![]() ,解得
,解得![]() ,
,
∴要使销售的总收入不低于原收入,每件定价最多为40元.
(2)依题意,当![]() 时,不等式
时,不等式![]() 有解,
有解,
即![]() 时,不等式
时,不等式![]() 有解.
有解.
∵![]()
![]() (当且仅当
(当且仅当![]() 时,等号成立),∴
时,等号成立),∴![]() .
.
∴当该商品明年的销售量![]() 至少达到10.2万件时,才可能使明年的销售收入不低于原收入与总收入之和,此时该商品的每件定价为30元.
至少达到10.2万件时,才可能使明年的销售收入不低于原收入与总收入之和,此时该商品的每件定价为30元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
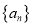 的前
的前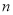 项和为
项和为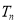 ,且
,且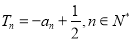 ,设
,设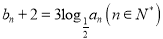 ,数列
,数列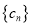 满足
满足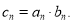 .
.(1)求数列
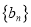 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和
项和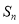 ;
;(3)若
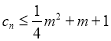 对一切正整数
对一切正整数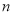 恒成立,求实数
恒成立,求实数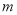 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】十一国庆节期间,某商场举行购物抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为
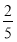 ,中奖可以获得3分;方案乙的中奖率为
,中奖可以获得3分;方案乙的中奖率为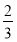 ,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.
,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为
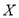 ,求
,求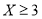 的概率;
的概率;(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,分别求两种方案下小明、小红累计得分的分布列,并指出为了累计得分较大,两种方案下他们选择何种方案较好,并给出理由?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为
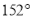 的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为
的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为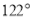 .半小时后,货轮到达C点处,观测到灯塔A的方位角为
.半小时后,货轮到达C点处,观测到灯塔A的方位角为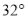 .求此时货轮与灯塔之间的距离.
.求此时货轮与灯塔之间的距离.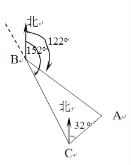
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
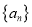 ,
, 满足:
满足: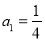 ,
,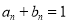 ,
,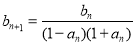 .
.(1)设
 ,求数列
,求数列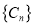 的通项公式;
的通项公式;(2)设
 ,不等式
,不等式 恒成立时,求实数
恒成立时,求实数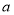 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
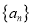 ,
,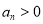 ,其前
,其前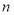 项和
项和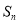 满足
满足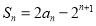 ,其中
,其中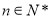 .
.(1)设
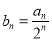 ,证明:数列
,证明:数列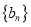 是等差数列;
是等差数列;(2)设
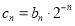 ,
,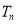 为数列
为数列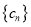 的前
的前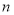 项和,求证:
项和,求证: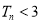 ;
;(3)设
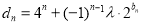 (
(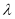 为非零整数,
为非零整数,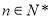 ),试确定
),试确定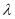 的值,使得对任意
的值,使得对任意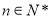 ,都有
,都有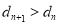 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
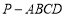 中,底面
中,底面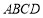 为菱形,
为菱形,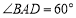 ,
,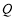 为
为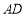 的中点.
的中点.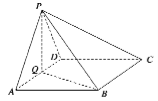
(1)若
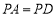 ,求证:
,求证: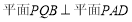 ;
;(2)若
 ,且
,且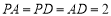 ,点
,点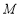 在线段
在线段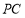 上,试确定点
上,试确定点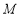 的位置,使二面角
的位置,使二面角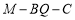 大小为
大小为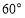 ,并求出
,并求出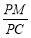 的值.
的值.
相关试题

