【题目】设函数![]() .
.
(1)当![]() 时,
时,![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,若函数
时,若函数![]() 在
在![]() 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数![]() 的取值范围;
的取值范围;
(3)是否存在常数![]() ,使函数
,使函数![]() 和函数
和函数![]() 在公共定义域上具有相同的单调性?若存在,求出
在公共定义域上具有相同的单调性?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)首先将问题转化为![]() 在
在![]() 上恒成立,然后令
上恒成立,然后令![]() ,从而通过求导研究函数
,从而通过求导研究函数![]() 的单调性,求得其最小值,进而求得
的单调性,求得其最小值,进而求得![]() 的取值范围;(2)首先将问题转化为
的取值范围;(2)首先将问题转化为![]() 在
在![]() 上恰有两个不同的零点,然后令
上恰有两个不同的零点,然后令![]() ,从而通过求导研究函数
,从而通过求导研究函数![]() 的单调性,求得其最小值,进而求得
的单调性,求得其最小值,进而求得![]() 的取值范围;(3)首先分别求得函数
的取值范围;(3)首先分别求得函数![]() 和函数
和函数![]() 的单调区间,然后根据
的单调区间,然后根据![]() 与
与![]() 具有相同的单调性建立关于
具有相同的单调性建立关于![]() 的不等式组,由此求得
的不等式组,由此求得![]() 的值.
的值.
试题解析:(1)当![]() 时,由
时,由![]() 得
得![]() ,
,
∵![]() ,∴
,∴![]() ,∴有
,∴有![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,由
,由![]() 得
得![]() ,
,
当![]() ,∴
,∴![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
∴![]() ,∴实数
,∴实数![]() 的取值范围为
的取值范围为![]() ;
;
(2)当![]() 时,函数
时,函数![]() ,
,
![]() 在
在![]() 上恰有两个不同的零点,即
上恰有两个不同的零点,即![]() 在
在![]() 上恰有两个不同的零点,
上恰有两个不同的零点,
令![]() ,则
,则![]() ,
,
当![]() ,
,![]() ;当
;当![]() ,
,![]() ,
,
∴![]() 在
在![]() 上单减,在
上单减,在![]() 上单增,
上单增,![]() ,
,
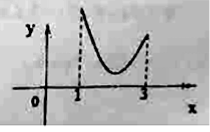
又![]() ,
,![]() 如图所示,所以实数
如图所示,所以实数![]() 的取值范围为
的取值范围为![]() .
.
(3)函数![]() 和函数
和函数![]() 在公共定义域为
在公共定义域为![]() ,
,
∴![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增,
上单调递增,
函数![]() ,
,
![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增,不合题意,
上单调递增,不合题意,
![]() 时,当
时,当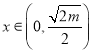 时
时![]() ,当
,当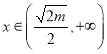 时,
时,![]() ,
,
![]() 在
在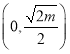 上单调递减,在
上单调递减,在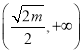 上为单调递增,
上为单调递增,
要使![]() 与
与![]() 具有相同的单调性,须
具有相同的单调性,须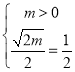 ,解得
,解得![]() .
.
存在常数![]() 时,使
时,使![]() 与
与![]() 具有相同的单调性.
具有相同的单调性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销量价格P(元)的关系如图所示;③每月需各种开支2 000元.
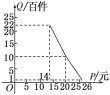
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆市某厂党支部10月份开展“两学一做”活动,将10名党员技工平均分为甲,乙两组进行技能比赛.要求在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
1号
2号
3号
4号
5号
甲组
4
5
7
9
10
乙组
5
6
7
8
9
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此分析两组技工的技术水平;
(2)质检部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,求该车间“质量合格”的概率.
-
科目: 来源: 题型:
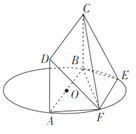
查看答案和解析>>【题目】如图,
 为圆
为圆 的直径,点
的直径,点 在圆
在圆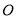 上,
上, 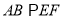 ,矩形
,矩形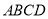 所在的平面与圆
所在的平面与圆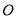 所以的平面互相垂直,已知
所以的平面互相垂直,已知 .
.(1)求证:平面
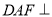 平面
平面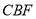 ;
;(2)当
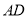 的长为何值时,平面
的长为何值时,平面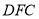 与平面
与平面 所成的锐二面角的大小为
所成的锐二面角的大小为 ?
?
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
以坐标原点为极点,以
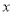 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线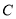 的参数方程为
的参数方程为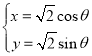 (
(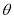 为参数,
为参数,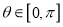 ),直线
),直线 的参数方程为
的参数方程为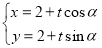 (
(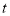 为参数).
为参数).(1)点
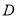 在曲线
在曲线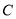 上,且曲线
上,且曲线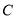 在点
在点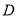 处的切线与直线
处的切线与直线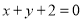 垂直,求点
垂直,求点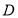 的极坐标;
的极坐标;(2)设直线
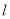 与曲线
与曲线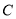 有两个不同的交点,求直线
有两个不同的交点,求直线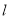 的斜率的取值范围.
的斜率的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1 ,正方形
 的边长为
的边长为 分别是
分别是 和
和 的中点,
的中点, 是正方形的对角线
是正方形的对角线 与
与 的交点,
的交点, 是正方形两对角线的交点,现沿
是正方形两对角线的交点,现沿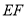 将
将 折起到
折起到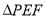 的位置,使得
的位置,使得 ,连结
,连结 (如图2).
(如图2).
(1)求证:
 ;
;(2)求三棱锥
 的高.
的高. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
 .
.(1)当
 时,解不等式
时,解不等式 ;
;(2)若
 ,求
,求 的取值范围.
的取值范围.
相关试题

