【题目】在古希腊毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形则第n个三角形数为 . 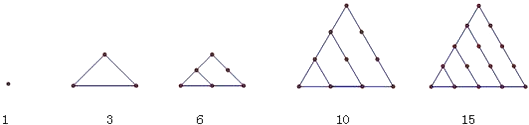
参考答案:
【答案】![]()
【解析】解:设第n个三角形数即第n个图中有an个点;
由图可得:
第二个图中点的个数比第一个图中点的个数多2,即a2﹣a1=2,
第三个图中点的个数比第二个图中点的个数多3,即a3﹣a2=3,
…
第n个图中点的个数比第n﹣1个图中点的个数多n,即an﹣an﹣1=n,
则an=1+2+3+4+…+n= ![]() ;
;
所以答案是 ![]() .
.
【考点精析】解答此题的关键在于理解归纳推理的相关知识,掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:日需求量n
14
15
16
17
18
19
20
频数
10
20
16
16
15
13
10
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设偶函数
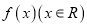 的导函数是函数
的导函数是函数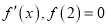 ,当
,当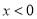 时,
时, 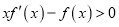 ,则使得
,则使得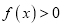 成立的
成立的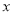 的取值范围是( )
的取值范围是( )A.
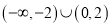 B.
B. 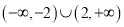
C.
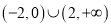 D.
D. 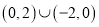
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a∈R,函数f(x)=x2﹣2ax+5.
(1)若a>1,且函数f(x)的定义域和值域均为[1,a],求实数a的值;
(2)若不等式x|f(x)﹣x2|≤1对x∈[ ,
,  ]恒成立,求实数a的取值范围.
]恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ln(2x+3)+x2
(1)讨论f(x)的单调性;
(2)求f(x)在区间[﹣ ,
,  ]的最大值和最小值.
]的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
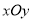 中,已知圆
中,已知圆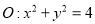 ,椭圆
,椭圆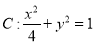 ,
, 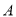 为椭圆
为椭圆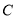 的右顶点,过原点且异于
的右顶点,过原点且异于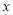 轴的直线与椭圆
轴的直线与椭圆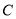 交于
交于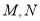 两点,
两点, 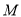 在
在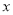 轴的上方,直线
轴的上方,直线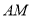 与圆
与圆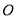 的另一交点为
的另一交点为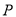 ,直线
,直线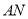 与圆
与圆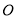 的另一交点为
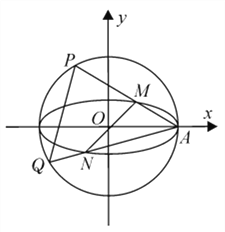
的另一交点为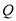 ,
,
(1)若
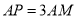 ,求直线
,求直线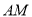 的斜率;
的斜率;(2)设
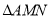 与
与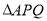 的面积分别为
的面积分别为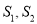 ,求
,求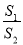 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)是R上的偶函数,且当x≤0时,f(x)=log
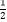 (1﹣x)+x.
(1﹣x)+x.
(1)求f(1)的值;
(2)求函数y=f(x)的表达式,并直接写出其单调区间(不需要证明);
(3)若f(lga)+2<0,求实数a的取值范围.
相关试题

