【题目】为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本,(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出如下频率分布直方图.
的分组作出如下频率分布直方图.
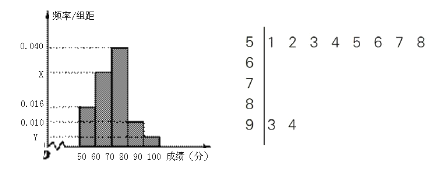
(1)由如下茎叶图(图中仅列出了得分在![]() ,
,![]() 的数据)提供的信息,求样本容量
的数据)提供的信息,求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国谜语大会”,求所抽取的2名学生中至少有一人得分在![]() 内的概率.
内的概率.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)从茎叶图中知![]() 这一组的人数是8,由频率可得总容量
这一组的人数是8,由频率可得总容量![]() ,接着由
,接着由![]() 这一组人数是2,可求得
这一组人数是2,可求得![]() ,再由频率分布直方图的性质可求得
,再由频率分布直方图的性质可求得![]() ;(2)分数在
;(2)分数在![]() 内的学生有5人,分数在
内的学生有5人,分数在![]() 内的学生有2人,可把他们编号,然后列举出从中取2人的所有组合,计算出总数及符号条件的数目,由古典概率公式可得概率.
内的学生有2人,可把他们编号,然后列举出从中取2人的所有组合,计算出总数及符号条件的数目,由古典概率公式可得概率.
试题解析:(1)由题意可知,样本容量![]() ,
,![]() ,
,
![]() .
.
(2)由题意可知,分数在![]() 内的学生有5人,记这5人分别为
内的学生有5人,记这5人分别为![]() ,
,![]() ,
,
分数在![]() 内的学生有2人,记这2人分别为
内的学生有2人,记这2人分别为![]() .
.
抽取的2名学生的所有情况有21种,分别为:
![]() ,
,
![]() ,
,
![]()
其中2名同学的分数都不在![]() 内的情况有10种,分别为:
内的情况有10种,分别为:
![]()
![]()
![]() ,
,
∴所抽取的2名学生中至少有一人得分在![]() 内的概率
内的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列推理中属于归纳推理且结论正确的是( )
A.由an=2n﹣1,求出S1=12 , S2=22 , S3=32 , …,推断:数列{an}的前n项和Sn=n2
B.由f(x)=xcosx满足f(﹣x)=﹣f(x)对?x∈R都成立,推断:f(x)=xcosx为奇函数
C.由圆x2+y2=r2的面积S=πr2 , 推断:椭圆 =1的面积S=πab
=1的面积S=πab
D.由(1+1)2>21 , (2+1)2>22 , (3+1)2>23 , …,推断:对一切n∈N* , (n+1)2>2n -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆心为C的圆经过O(0,0))和A(4,0)两点,线段OA的垂直平分线和圆C交于M,N两点,且|MN|=2
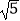
(1)求圆C的方程
(2)设点P在圆C上,试问使△POA的面积等于2的点P共有几个?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
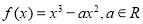 .
.(1)若
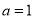 ,求曲线在
,求曲线在 点处的切线方程;
点处的切线方程;(2)若曲线
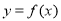 与直线
与直线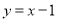 只有一个交点,求实数
只有一个交点,求实数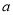 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在矩形
 中,
中,  ,
,  是
是 的中点,将三角形
的中点,将三角形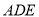 沿
沿 翻折到图②的位置,使得平面
翻折到图②的位置,使得平面
 平面
平面 .
.(1)在线段
 上确定点
上确定点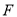 ,使得
,使得 平面
平面 ,并证明;
,并证明;(2)求
 与
与 所在平面构成的锐二面角的正切值.
所在平面构成的锐二面角的正切值. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PD⊥底面ABCD,点M、N分别是棱AB、CD的中点.
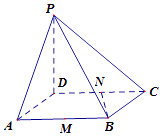
(1)证明:BN⊥平面PCD;
(2)在线段PC上是否存在点H,使得MH与平面PCD所成最大角的正切值为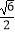 ,若存在,请求出H点的位置;若不存在,请说明理由.
,若存在,请求出H点的位置;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的半径为1,圆心C(a,2a﹣4),(其中a>0),点O(0,0),A(0,3)
(1)若圆C关于直线x﹣y﹣3=0对称,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点P,使|PA|=|2PO|,求圆心C的横坐标a的取值范围.
相关试题

