【题目】根据某电子商务平台的调查统计显示,参与调查的1 000位上网购物者的年龄情况如图所示.
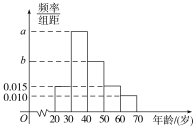
(1)已知[30,40),[40,50),[50,60)三个年龄段的上网购物者人数成等差数列,求a,b的值;
(2)该电子商务平台将年龄在[30,50)内的人群定义为高消费人群,其他年龄段的人群定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1 000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此3人获得代金券总和X(单位:元)的分布列与数学期望.
参考答案:
【答案】见解析
【解析】(1)由题意可知![]()
解得a=0.035,b=0.025.
(2)利用分层抽样从样本中抽取10人,易知其中属于高消费人群的有6人,属于潜在消费人群的有4人.
从该10人中抽取3人,此3人所获得代金券的总和为X(单位:元),
则X的所有可能取值为150,200,250,300.
P(X=150)=![]() =
=![]() ,
,
P(X=200)=![]() =
=![]() ,
,
P(X=250)=![]() =
=![]() ,
,
P(X=300)=![]() =
=![]() .
.
所以X的分布列为
X | 150 | 200 | 250 | 300 |
P |
|
|
|
|
E(X)=150×![]() +200×
+200×![]() +250×
+250×![]() +300×
+300×![]() =210.
=210.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作
不太主动参加班级工作
合计
学习积极性高
18
7
25
学习积极性一般
6
19
25
合计
24
26
50
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
参考公式与临界值表:K2=
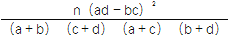 .
.P(K2≥k)
0.100
0.050
0.025
0.010
0.001
k
2.706
3.841
5.024
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂的甲、乙两个车间的
 名工人进行了劳动技能大比拼,规定:技能成绩大于或等于
名工人进行了劳动技能大比拼,规定:技能成绩大于或等于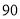 分为优秀,
分为优秀, 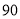 分以下为非优秀,统计成成绩后,得到如下的
分以下为非优秀,统计成成绩后,得到如下的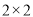 列联表,且已知在甲、乙两个车间工人中随机抽取
列联表,且已知在甲、乙两个车间工人中随机抽取 人为优秀的概率为
人为优秀的概率为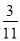 .
.优秀
非优秀
合计
甲车间
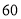
乙车间
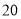
合计

(1)请完成上面的列联表;
(2)根据列联表的数据,若按
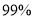 的可靠性要求,能否认为“成绩与车间有关系”?
的可靠性要求,能否认为“成绩与车间有关系”? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在坐标原点,焦点在
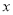 轴上的椭圆,离心率为
轴上的椭圆,离心率为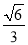 且过点
且过点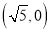 ,过定点
,过定点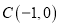 的动直线与该椭圆相交于
的动直线与该椭圆相交于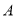 、
、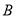 两点.
两点.(1)若线段
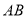 中点的横坐标是
中点的横坐标是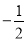 ,求直线
,求直线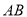 的方程;
的方程;(2)在
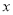 轴上是否存在点
轴上是否存在点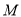 ,使
,使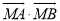 为常数?若存在,求出点
为常数?若存在,求出点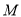 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期
4月1日
4月7日
4月15日
4月21日
4月30日
温差x/℃
10
11
13
12
8
发芽数y/颗
23
25
30
26
16
(1)从这5天中任选2天,记发芽的种子数分别为m,n,求事件“m,n均不小于25”的概率;
(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出y关于x的线性回归方程
 =
= x+
x+ ;
;(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
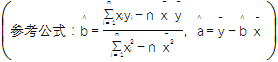
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在极坐标系中点C的极坐标为
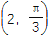 .
.(1)求出以点C为圆心,半径为2的圆的极坐标方程(写出解题过程)并画出图形;
(2)在直角坐标系中,以圆C所在极坐标系的极点为原点,极轴为x轴的正半轴建立直角坐标系,点P是圆C上任意一点,Q(5,-
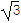 ),M是线段PQ的中点,当点P在圆C上运动时,求点M的轨迹的普通方程.
),M是线段PQ的中点,当点P在圆C上运动时,求点M的轨迹的普通方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acos θ(a>0),过点P(-2,-4)的直线l:
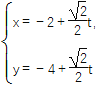 (t为参数)与曲线C相交于M,N两点.
(t为参数)与曲线C相交于M,N两点.(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求实数a的值.
相关试题

