【题目】已知椭圆E:![]() +
+![]() =1(a>b>0),其左右焦点为F1,F2,过F2的直线l交椭圆E于A,B两点,△AB F1的周长为8,且△AF1F2的面积最大时,△AF1F2为正三角形。
=1(a>b>0),其左右焦点为F1,F2,过F2的直线l交椭圆E于A,B两点,△AB F1的周长为8,且△AF1F2的面积最大时,△AF1F2为正三角形。
(1)求椭圆E的方程;
(2)若MN是椭圆E经过 原点的弦,MN||AB,求证: ![]() 为定值
为定值
参考答案:
【答案】(1)![]() (2)4
(2)4
【解析】试题分析:(I)根据题意列出关于![]() 、
、![]() 、
、![]() 的方程组,结合性质
的方程组,结合性质![]() , 求出
, 求出![]() 、
、![]() 、
、![]() ,即可得结果;(Ⅱ)直线与曲线联立,根据韦达定理,弦长公式将
,即可得结果;(Ⅱ)直线与曲线联立,根据韦达定理,弦长公式将![]() 用
用![]() 表示,消去
表示,消去![]() 即可得结果.
即可得结果.
试题解析:(I)由已知A,B在椭圆上,可得|AF1|+|AF2|=|BF1|=|BF2|=2a,
又△ABF1的周长为8,所以|AF1|+|AF2|+|BF1|=|BF2|=4a=8,即a=2,
由椭圆的对称性可得,△AF1F2为正三角形当且仅当A为椭圆短轴顶点,
则a=2c,即c=1,b2=a2﹣c2=3,
则椭圆C的方程为![]()
(Ⅱ)证明:若直线l的斜率不存在,即l:x=1,求得|AB|=3,|MN|=2![]() ,可得
,可得![]() =4;
=4;
若直线l的斜率存在,设直线l:y=k(x﹣1),
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
代入椭圆方程![]() +
+![]() ,可得(3+4k2)x2﹣8k2x+4k2﹣12=0,
,可得(3+4k2)x2﹣8k2x+4k2﹣12=0,
有x1+x2 =![]() ,x1x2=
,x1x2=![]() ,
,
|AB|![]() ,
,
由y=kx代入椭圆方程,可得x=±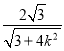 ,
,
|MN|=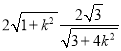
即有![]() =4.
=4.
综上可得![]() 为定值4.
为定值4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
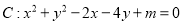
若
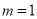 ,过点
,过点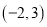 的直线
的直线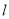 交曲线
交曲线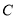 于
于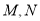 两点,且
两点,且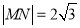 ,求直线
,求直线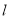 的方程;
的方程;若曲线
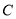 表示圆,且直线
表示圆,且直线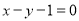 与圆
与圆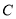 交于
交于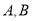 两点,是否存在实数
两点,是否存在实数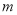 ,使得以
,使得以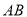 为直径的圆过原点,若存在,求出实数
为直径的圆过原点,若存在,求出实数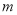 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列
 满足
满足 ,数列
,数列 满足
满足 .
. (1)求数列
 ,
,  的通项公式;
的通项公式;(2)令
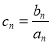 ,求数列
,求数列 的前
的前 项和
项和 ;
;(3)若
 ,求对所有的正整数
,求对所有的正整数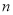 都有
都有 成立的
成立的 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁)
[15,25)
[25,35)
[35,45)
[45,55)
[55,65)
[65,75)
频数
5
10
15
10
5
5
赞成人数
5
10
12
7
2
1
(Ⅰ)若以“年龄45岁为分界点”,由以上统计数据完成下面
 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;年龄不低于45岁的人数
年龄低于45岁的人数
合计
赞成
不赞成
合计
(Ⅱ)若从年龄在[25,35)和[55,65)的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在[55,65)的概率.
参考数据如下:
附临界值表:
0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
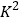 的观测值:
的观测值: 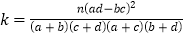 (其中
(其中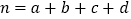 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次国际学术会议上,来自四个国家的五位代表被安排坐在一张圆桌,为了使他们能够自由交谈,事先了解到的情况如下:
甲是中国人,还会说英语.
乙是法国人,还会说日语.
丙是英国人,还会说法语.
丁是日本人,还会说汉语.
戊是法国人,还会说德语.
则这五位代表的座位顺序应为( )
A. 甲丙丁戊乙 B. 甲丁丙乙戊
C. 甲乙丙丁戊 D. 甲丙戊乙丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程.
已知曲线
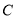 的参数方程为
的参数方程为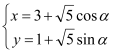 (
(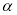 为参数),以直角坐标系原点为极点,
为参数),以直角坐标系原点为极点,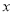 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.(1)求曲线
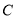 的极坐标方程;
的极坐标方程;(2)若直线的极坐标方程为
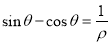 ,求直线被曲线
,求直线被曲线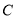 截得的弦长.
截得的弦长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(1)当
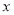 为常数,且
为常数,且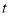 在区间
在区间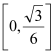 变化时,求
变化时,求 的最小值
的最小值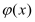 ;
;(2)证明:对任意的
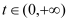 ,总存在
,总存在 ,使得
,使得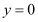 .
.
相关试题

