【题目】为方便市民休闲观光,市政府计划在半径为200![]() ,圆心角为
,圆心角为![]() 的扇形广场内(如图所示),沿△
的扇形广场内(如图所示),沿△![]() 边界修建观光道路,其中
边界修建观光道路,其中![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() 、
、![]() 两点间距离为定长
两点间距离为定长![]() .
.

(1)当![]() 时,求观光道
时,求观光道![]() 段的长度;
段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中![]() 、
、![]() 两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)在△![]() 中,由已知及正弦定理得
中,由已知及正弦定理得![]() ,即可求解观光道
,即可求解观光道![]() 段的长度;(2)设
段的长度;(2)设![]() ,
, ![]() ,在
,在![]() 中,由余弦定理,化简得出方程
中,由余弦定理,化简得出方程![]() ,再利用基本不等式,即可求解总长度的最大值.
,再利用基本不等式,即可求解总长度的最大值.
试题解析:(1)在△![]() 中,由已知及正弦定理得,
中,由已知及正弦定理得,
![]() ,即
,即![]() ,∴
,∴![]() .
.
(2)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
在△![]() 中,
中, ![]() ,即
,即![]() ,
,
所以![]() ,
,
故![]() ,当且仅当
,当且仅当![]() 时,
时, ![]() 取得最大值,
取得最大值,
所以当![]() 、
、![]() 两点各距
两点各距![]() 点60米处时,观光道路总长度最长,最长为
点60米处时,观光道路总长度最长,最长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x≤1,比较3x3与3x2-x+1的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c是两两不等的实数,则p=a2+b2+c2与q=ab+bc+ca的大小关系是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
以直角坐标系
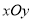 的原点为极点,
的原点为极点,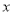 轴的非负半轴为极轴建立极坐标,且两坐标系取相同的长度单位.已知点
轴的非负半轴为极轴建立极坐标,且两坐标系取相同的长度单位.已知点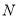 的极坐标为
的极坐标为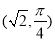 ,圆
,圆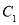 的极坐标方程为
的极坐标方程为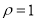 ,若
,若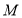 为曲线
为曲线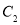 上的动点,且
上的动点,且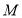 到定点
到定点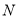 的距离等于圆
的距离等于圆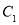 的半径.
的半径.(1)求曲线
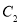 的直角坐标方程;
的直角坐标方程;(2)若过点
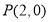 的直线
的直线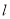 的参数方程为
的参数方程为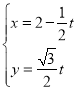 (
(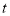 为参数),且直线
为参数),且直线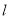 与曲线
与曲线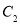 交于
交于 、
、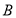 两点,求
两点,求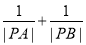 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
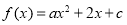 的对称轴为
的对称轴为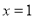 ,
,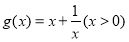 .
.(1)求函数
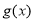 的最小值及取得最小值时
的最小值及取得最小值时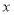 的值;
的值;(2)试确定
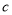 的取值范围,使
的取值范围,使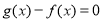 至少有一个实根;
至少有一个实根;(3)若
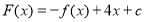 ,存在实数
,存在实数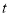 ,对任意
,对任意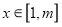 ,使
,使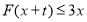 恒成立,求实数
恒成立,求实数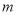 的取
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.

(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件2件作品获奖,问这两组哪一组获奖率较高?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的对称轴为
的对称轴为 ,
, .
.(1)求函数
 的最小值及取得最小值时
的最小值及取得最小值时 的值;
的值;(2)试确定
 的取值范围,使
的取值范围,使 至少有一个实根;
至少有一个实根;(3)当
 时,
时, ,对任意
,对任意 有
有 恒成立,求
恒成立,求 的取值范围.
的取值范围.
相关试题

