【题目】已知数列{an}的前n项和为Sn , 且Sn=2an﹣2,数列{bn}满足b1=1,且bn+1=bn+2.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ![]() ,求数列{cn}的前2n项和T2n .
,求数列{cn}的前2n项和T2n .
参考答案:
【答案】
(1)解:当n=1,a1=2;
当n≥2时,an=Sn﹣Sn﹣1=2an﹣2an﹣1,
∴an=2an﹣1.
∴{an}是等比数列,公比为2,首项a1=2,
∴ ![]() .
.
由bn+1=bn+2,得{bn}是等差数列,公差为2.
又首项b1=1,
∴bn=2n﹣1
(2)解: ![]()
∴ ![]() +[3+7+…+(4n﹣1)]
+[3+7+…+(4n﹣1)]
= ![]()
= ![]()
【解析】(1)当n=1,可求a1 , n≥2时,an=Sn﹣Sn﹣1可得an与an﹣1的递推关系,结合等比数列的通项公式可求an , 由bn+1=bn+2,可得{bn}是等差数列,结合等差数列的通项公式可求bn . (2)由题意可得 ![]() ,然后结合等差数列与等比数列的求和公式,利用分组求和即可求解
,然后结合等差数列与等比数列的求和公式,利用分组求和即可求解
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系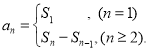 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列4个函数:①
 ;②y=sinx;③y=﹣tanx;④y=﹣cos2x、其中在区间
;②y=sinx;③y=﹣tanx;④y=﹣cos2x、其中在区间  上增函数且以π为周期的函数是(把所有符合条件的函数序列号都填上)
上增函数且以π为周期的函数是(把所有符合条件的函数序列号都填上) -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件。已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA=
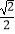 ,E为BC的中点.
,E为BC的中点. 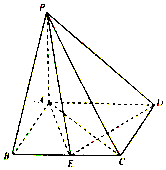
(1)证明:PE⊥ED;
(2)求二面角E﹣PD﹣A的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a∈R,解关于x的不等式ax2﹣(a+1)x+1<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
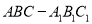 中,
中, 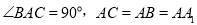 ,
, 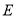 是
是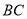 的中点,
的中点, 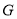 是
是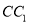 的中点。
的中点。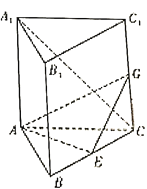
(1)求异面直线
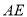 与
与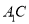 所成的角;
所成的角;(II)求证
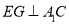
(III)求二面角
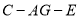 的正切值.
的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)讨论
 的单调性;
的单调性;(2)设
 ,当
,当 时,
时, ,求
,求 的最大值;
的最大值;(3)已知
 ,估计
,估计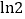 的近似值(精确到0.001)
的近似值(精确到0.001)
相关试题

