【题目】某公司为提高员工的综合素质,聘请专业机构对员工进行专业技术培训,其中培训机构费用成本为12000元.公司每位员工的培训费用按以下方式与该机构结算:若公司参加培训的员工人数不超过30人时,每人的培训费用为850元;若公司参加培训的员工人数多于30人,则给予优惠:每多一人,培训费减少10元.已知该公司最多有60位员工可参加培训,设参加培训的员工人数为![]() 人,每位员工的培训费为
人,每位员工的培训费为![]() 元,培训机构的利润为
元,培训机构的利润为![]() 元.
元.
(1)写出![]() 与
与![]()
![]() 之间的函数关系式;
之间的函数关系式;
(2)当公司参加培训的员工为多少人时,培训机构可获得最大利润?并求最大利润.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)根据题意,只要注意超过30人时,每多1人才能减少10元,因此可分类,![]() 和
和![]() (
(![]() ),在
),在![]() 时,培训费用为
时,培训费用为![]() ;
;
(2)利润是用每人的培训费用乘以培训人数减去成本12000,根据一次函数与二次函数的性质分类求得最大值,然后比较即得.
详解:(1)依题意得,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
![]() .
.
(2)当![]() 时,
时,![]() ,
,
![]() 时,
时, ![]() 取得最大值
取得最大值![]() .
.
当![]() 时,
时,
![]() ,
,
![]() ,
,
当![]() 或
或![]() 时,
时, ![]() 取得最大值
取得最大值![]() .
.
因为![]() ,
,
![]() 当公司参加培训的员工人数为
当公司参加培训的员工人数为![]() 或
或![]() 时,
时,
培训机构可获得最大利润![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛掷两枚骰子,求:
(1)点数之和为4的倍数的概率;
(2)点数之和大于5而小于10的概率;
(3)同时抛两枚骰子,求至少有一个5点或者6点的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数f(x)=
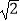 sin2x﹣
sin2x﹣ 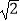 cos2x+1的图象向左平移
cos2x+1的图象向左平移  个单位,再向下平移1个单位,得到函数y=g(x)的图象,则下列关予函数y=g(x)的说法错误的是( )
个单位,再向下平移1个单位,得到函数y=g(x)的图象,则下列关予函数y=g(x)的说法错误的是( )
A.函数y=g(x)的最小正周期为π
B.函数y=g(x)的图象的一条对称轴为直线x=
C.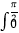 g(x)dx=
g(x)dx= 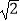
D.函数y=g(x)在区间[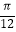 ,
, 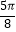 ]上单调递减
]上单调递减 -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,函数y=ax+a与y=ax的图象大致是( )
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】点M(3,2)到拋物线C:y=ax2(a>0)准线的距离为4,F为拋物线的焦点,点N(l,l),当点P在直线l:x﹣y=2上运动时,
 的最小值为( )
的最小值为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球
(I)试问:一共有多少种不同的结果?请列出所有可能的结果;
(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是
是 上的奇函数,且当
上的奇函数,且当 时,
时, ,
, .
.(1)若
 ,求
,求 的解析式;
的解析式;(2)若
 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)若
 的值域为
的值域为 ,求
,求 的取值范围.
的取值范围.
相关试题

