【题目】设![]() 是
是![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的解析式;
的解析式;
(2)若![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 的值域为
的值域为![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)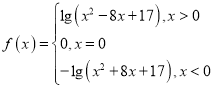 ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据![]() 求出参数,利用奇函数的定义
求出参数,利用奇函数的定义![]() 可求出当
可求出当![]() 时函数的解析式,由
时函数的解析式,由![]() 是
是![]() 上的奇函数可知
上的奇函数可知![]() ,即可写出函数解析式;(2)由
,即可写出函数解析式;(2)由![]() 可知当
可知当![]() 时,
时,![]() ,即可判断函数
,即可判断函数![]() 在
在![]() 上单调递增,由奇函数在对称的区间上单调性一致可知
上单调递增,由奇函数在对称的区间上单调性一致可知![]() 在
在![]() 上单调递增, 利用函数的单调性与奇偶性将
上单调递增, 利用函数的单调性与奇偶性将![]() 符号脱掉,转化为恒成立问题,即可求解;(3)首先使
符号脱掉,转化为恒成立问题,即可求解;(3)首先使![]() 对
对![]() 都有意义,由奇函数的图象与性质可知,要使
都有意义,由奇函数的图象与性质可知,要使![]() 的值域为
的值域为![]() ,则当
,则当![]() 时,使
时,使![]() 在第一象限及
在第一象限及![]() 的正半轴上都有图象,列出相应不等式即可.
的正半轴上都有图象,列出相应不等式即可.
(1)因为![]() ,则
,则![]() ,所以
,所以![]() .
.
所以当![]() 时,
时,![]() ,又
,又![]() ,故
,故
 .
.
(2)若![]() ,则
,则![]() 在
在![]() 上单调递增,故
上单调递增,故![]() 等价于
等价于
![]() ,令
,令![]() ,
,
于是![]() 在
在![]() 恒成立,
恒成立,
设![]() ,
,
①当![]() 时,则
时,则![]() ,于是
,于是![]() ,
,
②当![]() 时,则
时,则![]() ,得
,得![]() ,
,
综上,![]() .
.
(3)设![]() ,
,
首先![]() 对
对![]() 恒成立,
恒成立,
可得![]() 对
对![]() 恒成立,
恒成立,
故![]() .
.
由题意知,若函数![]() 的值域为
的值域为![]() ,
,
只需![]() 在
在![]() 上有解,即
上有解,即![]() 有解,
有解,
故有![]() ,
,
所以:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为提高员工的综合素质,聘请专业机构对员工进行专业技术培训,其中培训机构费用成本为12000元.公司每位员工的培训费用按以下方式与该机构结算:若公司参加培训的员工人数不超过30人时,每人的培训费用为850元;若公司参加培训的员工人数多于30人,则给予优惠:每多一人,培训费减少10元.已知该公司最多有60位员工可参加培训,设参加培训的员工人数为
 人,每位员工的培训费为
人,每位员工的培训费为 元,培训机构的利润为
元,培训机构的利润为 元.
元.(1)写出
 与
与
 之间的函数关系式;
之间的函数关系式;(2)当公司参加培训的员工为多少人时,培训机构可获得最大利润?并求最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点M(3,2)到拋物线C:y=ax2(a>0)准线的距离为4,F为拋物线的焦点,点N(l,l),当点P在直线l:x﹣y=2上运动时,
 的最小值为( )
的最小值为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球
(I)试问:一共有多少种不同的结果?请列出所有可能的结果;
(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】用数学归纳法证明“
 能被3整除”的第二步中,
能被3整除”的第二步中, 时,为了使用假设,应将5k+1-2k+1变形为( ).
时,为了使用假设,应将5k+1-2k+1变形为( ).A. (5k-2k)+4×5k-2k B. 5(5k-2k)+3×2k
C. (5-2)(5k-2k) D. 2(5k-2k)-3×5k
-
科目: 来源: 题型:
查看答案和解析>>【题目】有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)排成前后两排,前排3人,后排4人;(2)全体站成一排,甲不站排头也不站排尾;
(3)全体站成一排,女生必须站在一起;(4)全体站成一排,男生互不相邻.(用数字作答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在区间(0,+∞)内的单调函数,且对x∈(0,∞),都有f[f(x)﹣lnx]=e+1,设f′(x)为f(x)的导函数,则函数g(x)=f(x)﹣f′(x)的零点个数为( )
A.0
B.1
C.2
D.3
相关试题

