搜索
【题目】2002年北京国际数学家大会会标，是以中国古代数学家赵爽的弦图为基础而设计的，弦图用四个全等的直角三角形与一个小正方形拼成的一个大正方形
如图
，若大、小正方形的面积分别为25和1，直角三角形中较大锐角为
，则
等于
A. 
B. 
C. 
D. 
参考答案：
【答案】B
【解析】
根据两正方形的面积分别求出两正方形的边长，根据小正方形的边长等于直角三角形的长直角边减去短直角边，利用三角函数的定义表示出
，两边平方并利用同角三角函数间的基本关系及二倍角的正弦函数公式化简可得
的值，然后根据
的范围求出
的范围即可判断出
的正负，利用同角三角函数间的基本关系由即可求出的值．
大正方形面积为25，小正方形面积为1，
大正方形边长为5，小正方形的边长为1．
，
．
两边平方得：
，
．
是直角三角形中较小的锐角，
．
．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知数列
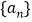的前n项和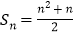
．
若三角形的三边长分别为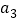
，
，
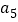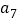，求此三角形的面积；
探究数列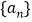中是否存在相邻的三项，同时满足以下两个条件：
此三项可作为三角形三边的长；
此三项构成的三角形最大角是最小角的2倍
若存在，找出这样的三项，若不存在，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知曲线C：
+ 
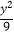=1，直线l： 
（t为参数）
（1）写出曲线C的参数方程，直线l的普通方程．
（2）过曲线C上任意一点P作与l夹角为30°的直线，交l于点A，求|PA|的最大值与最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系
中，椭圆
： 
的离心率是
，且直线
： 
被椭圆
截得的弦长为
．（Ⅰ）求椭圆
的标准方程；（Ⅱ）若直线
与圆
： 
相切：（i）求圆
的标准方程；（ii）若直线
过定点
，与椭圆
交于不同的两点
、
，与圆
交于不同的两点
、
，求
的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】设集合A={（x1 ， x2 ， x3 ， x4 ， x5）|xi∈{﹣1，0，1}，i={1，2，3，4，5}，那么集合A中满足条件“1≤|x1|+|x2|+|x3|+|x4|+|x5|≤3”的元素个数为（ ）
A.60
B.90
C.120
D.130 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知点A（2，0），抛物线C：x2=4y的焦点为F，射线FA与抛物线C相交于点M，与其准线相交于点N，则|FM|：|MN|=________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若等比数列{an}的各项均为正数，且a10a11+a9a12=2e5 ， 则lna1+lna2+…lna20= ．
相关试题
