【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]() 的离心率是
的离心率是![]() ,且直线
,且直线![]() :
: ![]() 被椭圆
被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 与圆
与圆![]() :
: ![]() 相切:
相切:
(i)求圆![]() 的标准方程;
的标准方程;
(ii)若直线![]() 过定点
过定点![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,与圆
,与圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(I)![]() ;(II)(i)
;(II)(i)![]() ;(ii)
;(ii)![]() .
.
【解析】试题分析:(Ⅰ)由直线![]() 过定点
过定点![]() ,
, ![]() ,可得到
,可得到![]() ,再结合
,再结合![]() ,即可求出椭圆的方程;(Ⅱ)(i)利用圆的几何性质,求出圆心到直线
,即可求出椭圆的方程;(Ⅱ)(i)利用圆的几何性质,求出圆心到直线![]() 的距离等于半径,即可求出
的距离等于半径,即可求出![]() 的值,即可求出圆
的值,即可求出圆![]() 的标准方程;(ii)首先设直线
的标准方程;(ii)首先设直线![]() 的方程为
的方程为![]() ,利用韦达定理即可求出弦长
,利用韦达定理即可求出弦长![]() 的表达式,同理利用圆的几何关系可求出弦长
的表达式,同理利用圆的几何关系可求出弦长![]() 的表达式,即可得到
的表达式,即可得到![]() 的表达式,再用换元法
的表达式,再用换元法![]() ,即可求出
,即可求出![]() 的取值范围.
的取值范围.
试题解析:
解:(Ⅰ)由已知得直线![]() 过定点
过定点![]() ,
, ![]() ,
, ![]() ,
,
又![]() ,
, ![]() ,解得
,解得![]() ,
, ![]() ,
,
故所求椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)(i)由(Ⅰ)得直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
又圆![]() 的标准方程为
的标准方程为![]() ,
,
∴圆心为![]() ,圆的半径
,圆的半径![]() ,
,
∴圆![]() 的标准方程为
的标准方程为![]() .
.
(ii)由题可得直线![]() 的斜率存在,
的斜率存在,
设![]() :
: ![]() ,与椭圆
,与椭圆![]() 的两个交点为
的两个交点为![]() 、
、![]() ,
,
由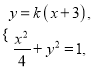 消去
消去![]() 得
得![]() ,
,
由![]() ,得
,得![]() ,
,
![]() ,
, ![]() ,
,
∴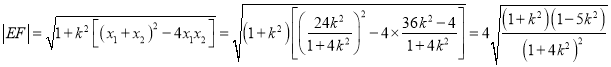 .
.
又圆![]() 的圆心
的圆心![]() 到直线
到直线![]() :
: ![]() 的距离
的距离![]() ,
,
∴圆![]() 截直线
截直线![]() 所得弦长
所得弦长![]() ,
,
∴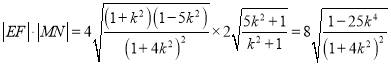 ,
,
设![]() ,
, ![]() ,
,
则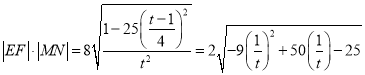 ,
,
∵![]() 的对称轴为
的对称轴为![]() ,在
,在![]() 上单调递增,
上单调递增, ![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)若
 ,求曲线
,求曲线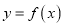 在点
在点 处的切线方程;
处的切线方程;(Ⅱ)若
 ,
,  恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(Ⅲ)当
 时,讨论函数
时,讨论函数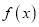 的单调性.
的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行六面体ABCD﹣A′B′C′D′,其中AB=4,AD=3,AA′=3,∠BAD=90°,∠BAA′=60°,∠DAA′=60°,则AC′的长为( )
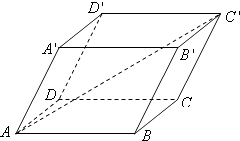
A.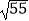
B.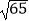
C.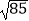
D.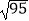
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3﹣3x+c有两个不同零点,且有一个零点恰为f(x)的极大值点,则c的值为( )
A.0
B.2
C.﹣2
D.﹣2或2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织了一次高二文科学生数学学业水平模拟测试,学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析,分别制成了如图所示的男生和女生数学成绩的频率分布直方图.

(Ⅰ)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?
(Ⅱ)在(Ⅰ)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意任取2人,求至少有一名男生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个说法: ①若向量{
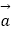 、
、 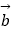 、
、 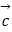 }是空间的一个基底,则{
}是空间的一个基底,则{ 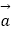 +
+ 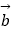 、
、 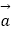 ﹣
﹣ 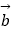 、
、 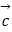 }也是空间的一个基底.
}也是空间的一个基底.
②空间的任意两个向量都是共面向量.
③若两条不同直线l,m的方向向量分别是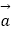 、
、 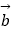 ,则l∥m
,则l∥m 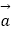 ∥
∥ 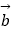 .
.
④若两个不同平面α,β的法向量分别是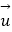 、
、 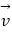 ,且
,且 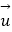 =(1,2,﹣2)、
=(1,2,﹣2)、 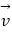 =(﹣2,﹣4,4),则α∥β.
=(﹣2,﹣4,4),则α∥β.
其中正确的说法的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=1+
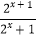 +sinx在区间[﹣k,k](k>0)上的值域为[m,n],则m+n=( )
+sinx在区间[﹣k,k](k>0)上的值域为[m,n],则m+n=( )
A.0
B.1
C.2
D.4
相关试题

