【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:t)和年利润
(单位:t)和年利润![]() (单位:千元)的影响.对近8年的年宣传费
(单位:千元)的影响.对近8年的年宣传费![]() 和年销售量
和年销售量![]() (i=1,2,…,8)数据作了初步处理,得到右面的散点图及一些统计量的值.
(i=1,2,…,8)数据作了初步处理,得到右面的散点图及一些统计量的值.

|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
, ![]()
(1)根据散点图判断, ![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的年利润![]() 与
与![]() 的关系为
的关系为![]() .根据(2)的结果回答下列问题:
.根据(2)的结果回答下列问题:
①年宣传费![]() =49时,年销售量及年利润的预报值是多少?
=49时,年销售量及年利润的预报值是多少?
②年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,
, ![]() …,
…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
![]()
参考答案:
【答案】(1)y=c+d![]() 适宜作为年销售量y关于年宣传费x的回归方程类型.(2)
适宜作为年销售量y关于年宣传费x的回归方程类型.(2)![]() =100.6+68
=100.6+68![]() .(3)①年销售量576.6,年利润预报值66.32.②年宣传费为46.24千元时,年利润的预报值最大.
.(3)①年销售量576.6,年利润预报值66.32.②年宣传费为46.24千元时,年利润的预报值最大.
【解析】(Ⅰ)由散点图可以判断,y=c+d![]() 适宜作为年销售量y关于年宣传费x的回归方程类型.
适宜作为年销售量y关于年宣传费x的回归方程类型.
(Ⅱ)令w=![]() ,先建立y关于w的线性回归方程.由于
,先建立y关于w的线性回归方程.由于

![]()
所以y关于w的线性回归方程为![]() =100.6+68w,
=100.6+68w,
因此y关于x的回归方程为![]() =100.6+68
=100.6+68![]() .
.
(Ⅲ) (ⅰ)由(Ⅱ)知,当x=49时,年销售量y的预报值
![]() =100.6+68
=100.6+68![]() =576.6,
=576.6,
年利润z的预报值![]() =576.6×0.2-49=66.32.
=576.6×0.2-49=66.32.
(ⅱ)根据(Ⅱ)的结果知,年利润z的预报值
![]() =0.2(100.6+68
=0.2(100.6+68![]() )-x=-x+13.6
)-x=-x+13.6![]() +20.12,
+20.12,
∴当![]() =
=![]() 即x=46.24时
即x=46.24时![]() 取最大值.
取最大值.
故宣传费用为46.24千元时,年利润的预报值最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
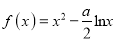 在点
在点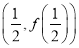 处的切线斜率为0.
处的切线斜率为0.(1)讨论函数
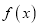 的单调性;
的单调性;(2)
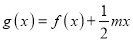 在区间
在区间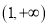 上没有零点,求实数
上没有零点,求实数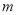 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
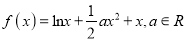 .
.
(Ⅰ)若f(1)=0,求函数f(x)的最大值;
(Ⅱ)令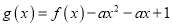 ,讨论函数g(x)的单调区间;
,讨论函数g(x)的单调区间;
(Ⅲ)若a=2,正实数x1,x2满足 证明
证明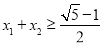
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形ABCD中,AB=3,AD=4.现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.
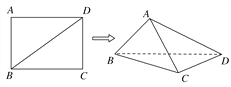
(1)试问:在折叠的过程中,直线AB与CD能否垂直?若能,求出相应a的值;若不能,请说明理由;
(2)求四面体A-BCD体积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
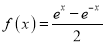 .
.(1)判断
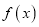 的奇偶性;
的奇偶性;(2)用单调性的定义证明
 为
为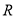 上的增函数;
上的增函数;(3)若对任意的
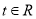 ,不等式
,不等式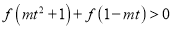 恒成立,求实数
恒成立,求实数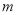 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一种新型的洗衣液,去污速度特别快.已知每投放k(1≤k≤4,且k∈R)个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度y(克/升)随着时间x(分钟)变化的函数关系式近似为y=k·f(x),其中f(x)=
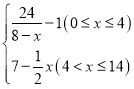 若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.(1)若只投放一次k个单位的洗衣液,两分钟时水中洗衣液的浓度为3(克/升),求k的值;
(2)若只投放一次4个单位的洗衣液,则有效去污时间可达几分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-
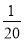 (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.

相关试题

