(本题满分14分)某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要 维护费50元.
维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多 少?
少?
参考答案:
解:(1)当每辆车的月租金定为3600元时,未租出的车辆数为: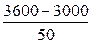 =12,所以这时租出了88辆车………………………………………………………………………..…4分
=12,所以这时租出了88辆车………………………………………………………………………..…4分
(2)设每辆车的月租金定为x元,则租赁公司的月收益为:
f( x)=(100-
x)=(100-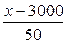 )(x-150)-
)(x-150)-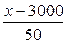 ×50,…………….…….……....10分
×50,…………….…….……....10分
整理得f(x)=-
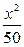 +162x-21000=-
+162x-21000=-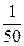 (x-4050)2+307050……………………...12分
(x-4050)2+307050……………………...12分
所以,当x=4050时,f(x)最大,其最大值为f(4050)=307050.
即当每辆车月租金定为4050元时,租赁公司月收益最大,最大收益为307050元.………..14分
解析
-
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分13
 分) 2010年11月在广州召开亚
分) 2010年11月在广州召开亚 运会,某小商品公司开发一种亚运会纪念品,每件产品的成本是15元,销售价是20元,月平
运会,某小商品公司开发一种亚运会纪念品,每件产品的成本是15元,销售价是20元,月平 均销售a件,通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明:如果产品的销售价提高的百分率为x(0<x<1),那么月平均
均销售a件,通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明:如果产品的销售价提高的百分率为x(0<x<1),那么月平均 销售量减少的百分率为x2,记改进工艺后,该公司销售纪念品的月平均利润是y(元).
销售量减少的百分率为x2,记改进工艺后,该公司销售纪念品的月平均利润是y(元).
(1)写出y与x的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使该公司销售该纪念品的月平均利润最大. -
科目: 来源: 题型:解答题
查看答案和解析>>(本题满分12分)
已知函数 (
(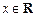 ),
),
(1)求函数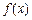 的最小值;
的最小值;
(2)已知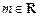 ,命题p:关于x的不等式
,命题p:关于x的不等式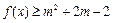 对任意
对任意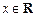 恒成立;命题q:不等式
恒成立;命题q:不等式 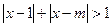 对任意
对任意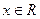 恒成立.若“p或q”为真,“p且q”为假,求实数m的取值范围.
恒成立.若“p或q”为真,“p且q”为假,求实数m的取值范围. -
科目: 来源: 题型:解答题
查看答案和解析>>(本题满分12分)已知函数
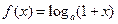 ,
,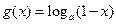 ,其中
,其中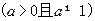 ,设
,设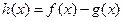
(1)判断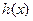 的奇偶性,并说明理由
的奇偶性,并说明理由
(2)若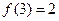 ,求使
,求使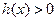 成立的x的集合
成立的x的集合 -
科目: 来源: 题型:解答题
查看答案和解析>>已知f(x)
 =x2+2x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的表达式.
=x2+2x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的表达式. -
科目: 来源: 题型:解答题
查看答案和解析>>(本题满分12分)二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;(2)若f(x)在区间[2a,a+1]上不单调,求a的取值范围. -
科目: 来源: 题型:解答题
查看答案和解析>>(本题满分12分)某网民用电脑上因特网有两种方案可选:一是在家里上网,费用分为通讯费(即电话费)与网络维护费两部分。现有政策规定:通讯费为0.02元/分钟,但每月30元封顶(即超过30元则只需交30元),网络维护费1元/小时,但每月上网不超过10小时则要交10元;二是到附近网吧上网,价格为1.5元/小时。
(1)将该网民在某月内在家上网的费用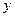 (元)表示为时间
(元)表示为时间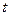 (小时)的函数;
(小时)的函数;
(2)试确定在何种情况下,该网民在家上网更便宜?
相关试题

