【题目】选修4-4;坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
参考答案:
【答案】(1)![]() ,
, ![]() (2)
(2)![]()
【解析】试题分析: (Ⅰ) 消去![]() 得直线
得直线![]() 的普通方程为
的普通方程为![]() . 由极坐标与直角坐标互化公式
. 由极坐标与直角坐标互化公式 ![]() ,可得曲线
,可得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() , 即
, 即![]() .
.
(Ⅱ) 设曲线![]() 上的点为
上的点为![]() ,
,
则点![]() 到直线
到直线![]() 的距离为
的距离为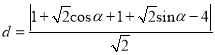
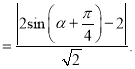 当
当![]() 时,
时, ![]() , 可得曲线
, 可得曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.
试题解析:
(Ⅰ) 由![]() 消去
消去![]() 得
得![]() ,
,
所以直线![]() 的普通方程为
的普通方程为![]() .
.
由![]() ,
,
得![]() .
.
将![]() 代入上式,
代入上式,
得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() , 即
, 即![]() .
.
(Ⅱ) 法1:设曲线![]() 上的点为
上的点为![]() ,
,
则点![]() 到直线
到直线![]() 的距离为
的距离为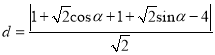
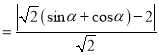
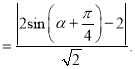
当![]() 时,
时, ![]() ,
,
所以曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.
法2: 设与直线![]() 平行的直线为
平行的直线为![]() ,
,
当直线![]() 与圆
与圆![]() 相切时, 得
相切时, 得![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
所以直线![]() 的方程为
的方程为![]() .
.
所以直线![]() 与直线
与直线![]() 的距离为
的距离为![]() .
.
所以曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线y=Asin(ωx+φ)(A>0,ω>0)上的一个最高点的坐标为(
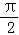 ,
,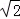 ),由此点到相邻最低点间的曲线与x轴交于点(
),由此点到相邻最低点间的曲线与x轴交于点(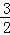 π,0),φ∈(﹣
π,0),φ∈(﹣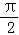 ,
,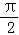 ).
).(1)求这条曲线的函数解析式;
(2)写出函数的单调区间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】共享单车是城市慢行系统的一种模式创新,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数
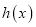 ,其中
,其中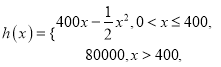
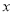 是新样式单车的月产量(单位:件),利润
是新样式单车的月产量(单位:件),利润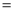 总收益
总收益 总成本.
总成本.(1)试将自行车厂的利润
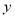 元表示为月产量
元表示为月产量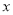 的函数;
的函数;(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,我国电子商务蓬勃发展. 2016年“618”期间,某网购平台的销售业绩高达516亿元人民币,与此同时,相关管理部门推出了针对该网购平台的商品和服务的评价系统. 从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.6,对服务的满意率为0.75,其中对商品和服务都满意的交易为80次.
(Ⅰ) 根据已知条件完成下面的
 列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?
列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?对服务满意
对服务不满意
合计
对商品满意
80
对商品不满意
合计
200
(Ⅱ) 若将频率视为概率,某人在该网购平台上进行的3次购物中,设对商品和服务都满意的次数为随机变量
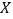 ,求
,求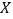 的分布列和数学期望
的分布列和数学期望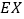 .
.附:
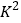
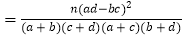 (其中
(其中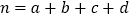 为样本容量)
为样本容量)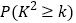
0.15
0.10
0.05
0.025
0.010
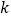
2.072
2.706
3.841
5.024
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)在某一个周期内的图象时,列表并填入的数据如下表:
x
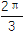
x1
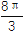
x2
x3
ωx+φ
0
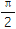
π
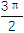
2π
Asin(ωx+φ)
0
2
0
-2
0
(1)求x1,x2,x3的值及函数f(x)的表达式;
(2)将函数f(x)的图象向左平移π个单位,可得到函数g(x)的图象,求函数y=f(x)·g(x)在区间
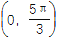 的最小值.
的最小值. -
科目: 来源: 题型:
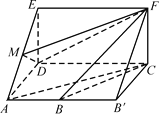
查看答案和解析>>【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,
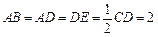 ,M是线段AE上的动点.
,M是线段AE上的动点.(1)试确定点M的位置,使AC∥平面MDF,并说明理由;
(2)在(1)的条件下,求平面MDF将几何体ADE-BCF分成的两部分的体积之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分形几何学是数学家伯努瓦·曼德尔布罗在
 世纪
世纪 年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图所示的分形规律可得如图乙所示的一个树形图:
年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图所示的分形规律可得如图乙所示的一个树形图:若记图乙中第
 行白圈的个数为
行白圈的个数为 ,则
,则 __________.
__________.
相关试题

