【题目】已知二次函数![]() 在
在![]() 处取得极值,且在
处取得极值,且在![]() 点处的切线与直线
点处的切线与直线![]() 平行.
平行.
(1)求![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递增区间及极值。
的单调递增区间及极值。
(3)求函数![]() 在
在![]() 的最值。
的最值。
参考答案:
【答案】(1)![]() .
.
(2)增区间为![]() ,
,![]() .在
.在![]() 有极小值为0。在
有极小值为0。在![]() 有极大值4/27。
有极大值4/27。
(3)![]() 的最大值为2,最小值为0。
的最大值为2,最小值为0。
【解析】试题分析:(1)第一步,求函数的导数,第二步:根据![]() 处取得极值,知
处取得极值,知![]() ,根据导数的几何意义知;在
,根据导数的几何意义知;在![]() 处的导数等于
处的导数等于![]() ,解得
,解得![]() ,第三步,代入写出
,第三步,代入写出![]() ,令
,令![]() ,得到极值点,最后,解出
,得到极值点,最后,解出![]() ;(2)根据(1)得到的结论,可知
;(2)根据(1)得到的结论,可知![]() 上的单调性,以及极值,比较端点值和极值的大小,就得到最大值和最小值.
上的单调性,以及极值,比较端点值和极值的大小,就得到最大值和最小值.
试题解析:解:(1) 由![]() ,可得
,可得![]() .由题设可得
.由题设可得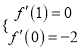
即![]() .解得
.解得![]() ,
, ![]() .所以
.所以![]() .
.
由题意得![]()
所以![]() .
.
令![]() ,得
,得![]() ,
, ![]() .
.
当![]() 变化时,
变化时, ![]() ,
, ![]() 变化情况如下表:
变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| 单调递增 | 4/27 | 单调递减 | 0 | 单调递增 |
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() .
.
(2)因为在![]() 时函数
时函数![]() 有极小值为0.在
有极小值为0.在![]() 时函数
时函数![]() 有极大值
有极大值![]() .
.
又![]() ,
,
所以函数![]() 的最大值为2,最小值为0.
的最大值为2,最小值为0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在调查运动员是否服用过兴奋剂的时候,给出两个问题作答,无关紧要的问题是:“你的身份证号码的尾数是奇数吗?”敏感的问题是:“你服用过兴奋剂吗?”然后要求被调查的运动员掷一枚硬币,如果出现正面,就回答第一个问题,否则回答第二个问题.由于回答哪一个问题只有被测试者自己知道,所以应答者一般乐意如实地回答问题.若我们把这种方法用于300个被调查的运动员,得到80个“是”的回答,则这群运动员中服用过兴奋剂的百分率大约为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设人的某一特征(如眼睛的大小)是由他的一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:
(1)1个孩子显露显性特征的概率是多少?
(2)“该父母生的2个孩子中至少有1个显露显性特征”,这种说法正确吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】调查在
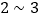 级风的海上航行中71名乘客的晕船情况,在男人中有12人晕船,25人不晕船,在女人中有10人晕船,24人不晕船
级风的海上航行中71名乘客的晕船情况,在男人中有12人晕船,25人不晕船,在女人中有10人晕船,24人不晕船 (1)作出性别与晕船关系的列联表;
(2)根据此资料,能否在犯错误的概率不超过0.1的前提下认为
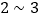 级风的海上航行中晕船与性别有关?
级风的海上航行中晕船与性别有关?晕船
不晕船
总计
男人
女人
总计
附:.
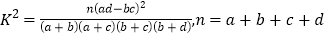
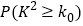
0.25
0.15
0.10
0.05
0.025

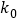
1.323
2.072
2.706
3.841
5.024
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为
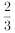 和
和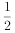 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中: (1)两种大树各成活1株的概率;
(2)成活的株数ξ的分布列与期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人做游戏,下列游戏不公平的是( )
A. 抛掷一枚骰子,向上的点数为奇数则甲获胜,向上的点数为偶数则乙获胜
B. 同时抛掷两枚硬币,恰有一枚正面向上则甲获胜,两枚都正面向上则乙获胜
C. 从一副不含大小王的扑克牌中抽一张,扑克牌是红色的则甲获胜,扑克牌是黑色的则乙获胜
D. 甲、乙两人各写一个数字1或2,如果两人写的数字相同甲获胜,否则乙获胜
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系
 中,椭圆
中,椭圆 :
: 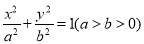 的离心率为
的离心率为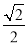 ,过椭圆右焦点
,过椭圆右焦点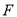 作两条互相垂直的弦,当其中一条弦所在直线斜率为0时,两弦长之和为6.
作两条互相垂直的弦,当其中一条弦所在直线斜率为0时,两弦长之和为6.(1)求椭圆的方程;
(2)
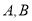 是抛物线
是抛物线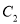 :
: 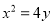 上两点,且
上两点,且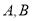 处的切线相互垂直,直线
处的切线相互垂直,直线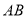 与椭圆
与椭圆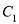 相交于
相交于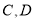 两点,求弦
两点,求弦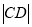 的最大值.
的最大值.
相关试题

