【题目】设函数![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 且
且![]() ,求证:
,求证:![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
参考答案:
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析: (1)已知单调区间求参数的取值范围,将问题转化为函数的最值问题;
(2)研究函数的零点,用零点存在性定理、数形结合思想求解.
试题解析:(1)∵![]() ,∴
,∴![]() ,
,
若![]() ,且
,且![]() 在区间
在区间![]() 上单调递增,
上单调递增,
则![]() 对任意的
对任意的![]() 恒成立,即
恒成立,即![]() 对任意的
对任意的![]() 恒成立,
恒成立,
∴![]() ,即实数
,即实数![]() 的取值范围为
的取值范围为![]() .
.
(2)当![]() 时,
时,![]() ,∴
,∴![]() ,
,
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() .∴
.∴![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,且
上单调递减,且![]() ,
,
∴![]() 在区间
在区间![]() 上有且仅有一个零点,
上有且仅有一个零点,
当![]() 时,
时,![]() ,∴
,∴![]() 在区间
在区间![]() 上单调递减,
上单调递减,
又![]() ,
,![]() ,
,
∴![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
综上,若![]() 且
且![]() ,则
,则![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
点晴:本题主要考查的是利用导数研究函数的单调性以及零点的个数,对逻辑思维能力、数形结合思想要求很高,属于难题.第(1)问已知单调区间求参数的取值范围,将含参函数问题转化为确定函数的最值问题;第(2)问研究函数的零点,用零点存在性定理、数形结合思想求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,直线l的方程为x﹣y+4=0,曲线C的参数方程为
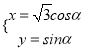 .
.(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为
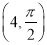 ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
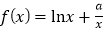 .
.(1)当
 时,证明函数
时,证明函数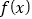 在
在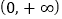 是单调函数;
是单调函数;(2)当
 时,函数
时,函数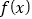 在区间
在区间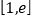 上的最小值是
上的最小值是 ,求
,求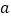 的值;
的值;(3)设
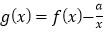 ,
,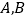 是函数
是函数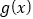 图象上任意不同的两点,记线段
图象上任意不同的两点,记线段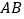 的中点的横坐标是
的中点的横坐标是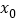 ,证明直线
,证明直线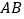 的斜率
的斜率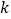
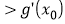 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)如图,曲线
 由上半椭圆
由上半椭圆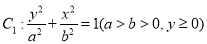 和部分抛物线
和部分抛物线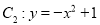
 连接而成,
连接而成, 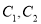 的公共点为
的公共点为 ,其中
,其中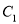 的离心率为
的离心率为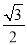 .
.
(Ⅰ)求
 的值;
的值;(Ⅱ)过点
 的直线
的直线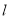 与
与 分别交于
分别交于 (均异于点
(均异于点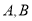 ),若
),若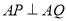 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)试判断函数
 的单调性;
的单调性;(2)设
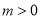 ,求
,求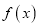 在
在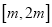 上的最大值;
上的最大值;(3)试证明:对任意
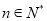 ,不等式
,不等式 都成立(其中
都成立(其中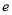 是自然对数的底数).
是自然对数的底数). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)判断并证明函数
 的奇偶性;
的奇偶性;(2)判断当
 时函数
时函数 的单调性,并用定义证明;
的单调性,并用定义证明;(3)若
 定义域为
定义域为 ,解不等式
,解不等式 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
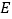 :
: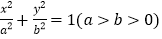 与
与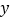 轴的正半轴相交于点
轴的正半轴相交于点 ,点
,点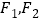 为椭圆的焦点,且
为椭圆的焦点,且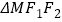 是边长为2的等边三角形,若直线
是边长为2的等边三角形,若直线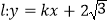 与椭圆
与椭圆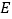 交于不同的两点
交于不同的两点 .
.(1)直线
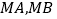 的斜率之积是否为定值?若是,请求出该定值;若不是,请说明理由;
的斜率之积是否为定值?若是,请求出该定值;若不是,请说明理由;(2)求
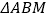 的面积的最大值.
的面积的最大值.
相关试题

