【题目】某工厂制作仿古的桌子和椅子,需要木工和漆工两道工序.已知生产一把椅子需要木工4个工作时,漆工2个工作时;生产一张桌子需要木工8个工作时,漆工1个工作时.生产一把椅子的利润为1500元,生产一张桌子的利润为2000元.该厂每个月木工最多完成8000个工作时、漆工最多完成1300个工作时.根据以上条件,该厂安排生产每个月所能获得的最大利润是__________元.
参考答案:
【答案】2100000
【解析】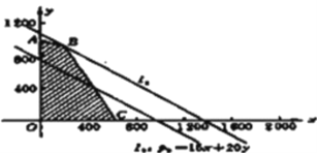
设每天生产桌子![]() 张,椅子
张,椅子![]() 张,利润总额为
张,利润总额为![]() ,目标函数为
,目标函数为![]() ,则
,则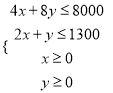 作出可行域,把直线
作出可行域,把直线![]() 向右上方平移至
向右上方平移至![]() 的位置时,直线经过可行域上的点
的位置时,直线经过可行域上的点![]() ,此时
,此时![]() 取最大值,解方程
取最大值,解方程![]() 得
得![]() 坐标为
坐标为![]() ,
, ![]() ,所以每天应生产桌子
,所以每天应生产桌子![]() 张,椅子
张,椅子![]() 张才能获得最大利润,最大利润为
张才能获得最大利润,最大利润为![]() ,故答案为
,故答案为![]() .
.
【方法点晴】本题主要考查利用线性规划解决现实生活中的最佳方案及最大利润问题,属于难题题. 求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
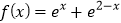 ,若关于
,若关于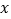 的不等式
的不等式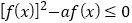 恰有3个整数解,则实数
恰有3个整数解,则实数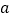 的最小值为( )
的最小值为( )A. 1 B.
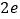 C.
C. 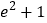 D.
D. 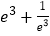
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  ,
,  .
.(1)若
 是
是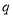 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围;
的取值范围;(2)若
 ,“
,“ ”为真命题,“
”为真命题,“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=ex-ax-1.
(1)求f(x)的单调增区间;
(2)若f(x)在定义域R内单调递增,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
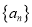 前
前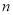 项和为
项和为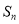 ,且
,且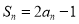 .
.(1)证明数列
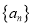 是等比数列;
是等比数列;(2)设
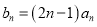 ,求数列
,求数列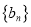 的前
的前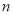 项和
项和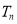 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着“互联网+交通”模式的迅猛发展,“共享自行车”在很多城市相继出现.某运营公司为了了解某地区用户对其所提供的服务的满意度,随机调查了40个用户,得到用户的满意度评分如下:

用系统抽样法从40名用户中抽取容量为10的样本,且在第一分段里随机抽到的评分数据为92.
(1)请你列出抽到的10个样本的评分数据;
(2)计算所抽到的10个样本的均值
 和方差
和方差 ;
;(3)在(2)条件下,若用户的满意度评分在
 之间,则满意度等级为“
之间,则满意度等级为“ 级”.试应用样本估计总体的思想,估计该地区满意度等级为“
级”.试应用样本估计总体的思想,估计该地区满意度等级为“ 级”的用户所占的百分比是多少?(精确到
级”的用户所占的百分比是多少?(精确到 )
)参考数据:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
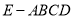 中,
中, 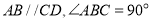 ,
,  ,点
,点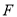 为棱
为棱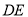 的中点.
的中点.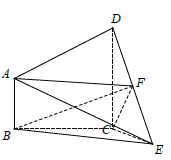
(1)证明:
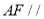 平面
平面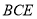 ;
; (2)若
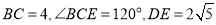 ,求三棱锥
,求三棱锥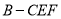 的体积.
的体积.
相关试题

